QbSyst2e.20.html
Système du Québécium
Suivant QbSyst2e.21.html
Précédent
QbSyst2e.19.htmlDébut QbSyst2e.1.html
Chapitre 12
Application à la classification des éléments
Tableaux bidimensionnels nouveaux

Fig. 242.
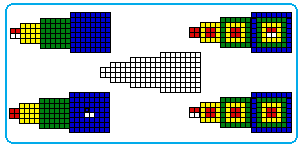
À la conquête d'une 2e dimension par pliage et collage des tableaux de Mendeleev existants.
Les tableaux de Mendeleev sont bâtis sur le postulat de la monodimensionnalité. Uniquement afin de marquer la périodicité, ils introduisent des alinéas en fin de période. Leurs périodes sont linéaires et parallèles sans déviation. Eut-on connu dès le dèbut les périodes tellement longues qu'elles ont requis des alinéas intérieurs, qu'on aurait peut-être pensé à exploiter davantage les ressources bidimensionnelles du plan.

Fig. 243. Un dessin linéaire de l'être humain donne une évocation plus ressemblante si l'on fait usage de 2 dimensions.
Fig. 244. Chromosomes en équerres pendant la mitose.
Le dessin d'une ligne droite peut suggèrer l'être humain, mais si on exploite 2 dimensions, la suggestion ressemble davantage à la vie. Figure 243.
Les chromosomes prennent des aspects tantôt filiformes et tantôt en équerres pendant la mitose. Figure 244.
Ces rappels, simplement pour dire qu'après pratiqué l'alignement en ligne droite pendant plus d'un siècle, il serait temps qu'on essaie un schéma en équerre avec angle droit, surtout si on a devant soi un jeu de cases carrées disponibles dans un damier indéfini.
La période 2 en équerres.
Commençons par la période 2, modèle idéal d'une période dans le tableau de Mendeleev. Figure 245.
Nous l'imaginons placée dans une grille indéfinie. Le chapitre précédent nous a appris l'existence des blocs s et p dans cette période. Cela nous facilite la tâche de déterminer des équerres dans cette période. Les 6 cases p se prêtent à former des équerres de cases contiguës, une possibilité parmi d'autres étant celle représentée.
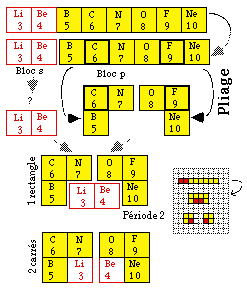
Fig. 245. Mise en équerres de la période 2. Rectangle et carrés. Les cases C et F sont les articulations du pliage. Pliage.
Quant aux cases s, il n'apparaît pas de recette évidente pour en former une équerre puisqu'elles sont seulement 2. Il faut un minimum de 3 cases pour former une équerre de cases contigües. Nous les laissons telles quelles pour le moment.
Le groupement unique le plus compact possible de ces 8 cases dessine un rectangle 2X4. Il est possible d'en former 2 groupements compacts carrés, contenant 1 case s et 3 cases p.
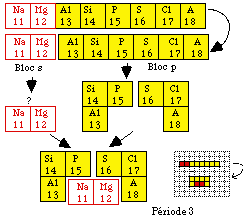
Fig. 246. Mise en équerres de la période 3.
La période 3 en équerres.
Nous pouvons très bien procéder de la même manière pour la période 3. Figure 246.
Le résultat, pour la période 3 comme pour la période 2, est un autre tableau rectangulaire où la succession des numéros atomiques est irrégulière. Chaque assemblage est 2X4, 2 cases en hauteur et 4 en langueur.
En collant les deux rectangles l'un en dessous de l'autre, nous obtenons un carré 4X4 . Figure 247.
Ce carré possède ou peut acquérir plusieurs attributs de symétrie. Par un retournement du bloc p de la période 3, il apparaît une couronne continue de 12 cases toutes p entourant 4 cases toutes s. Ce carré de 16 cases est un tableau de 16 cases ou une strate 2 telle que définie au chapitre 1, figure 13. (Cependant l'appellation strate 2 évoque la présence de strates voisines 1 de 4 cases et 3 de 36 cases, ce qui n'est pas le cas ici).
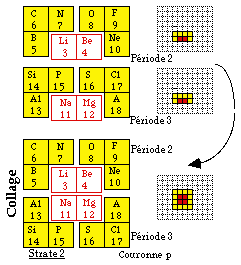
Fig. 247. Périodes 2 et 3 mises en tableau carré par collage.
Fermeture. Une périodicité d'une nouvelle sorte.
La couronne de cases p possède un attribut géométrique remarquable : elle est fermée, elle forme un circuit fermé. Cela est vrai pour la couronne résultant des cases des blocs p des périodes 2 et 3 réunies. Il n'est pas possible de réaliser une couronne fermée à partir des 6 cases p d'une seule période.
Nous avons ainsi fait apparaître une nouvelle sorte de périodicité, celle résultant de la circularité des cases p soumises au procédé géométrique décrit. Elle n'apparaît que si on réunit, dans cette opération, 2 périodes, les périodes 2 et 3.
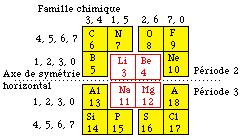
Fig. 248. Strate 2, familles chimiques, correspondance entre les colonnes de Mendeleev et l'alignement des cases. 2 familles chimiques par colonnes ou 4 familles chimiques par rangée avec répétition. Réf. fig. 241.
La périodicité nouvelle consiste en ceci : si on passe consécutivement d'une case à la suivante dans la couronne, on revient à la case de départ. Dans le langage des graphes : si on remplace les cases par des points appelés sommets, les arêtes reliant les sommets consécutifs tracent une ligne fermée sur elle-même.
On peut voir là une suggestion de considérer que la réunion de ces 2 périodes forme une entité distincte.
Les familles chimiques.
On repère facilement, dans ce tableau de 16 cases, les 8 familles chimiques de la figure 241. Figure 248. Les colonnes sont remplacées par des paires de cases alignées et symétriquement placées par rapport à un axe horizontal. Il y a 2 ou 4 familles chimiques par alignement. Les valeurs de Z croissent de gauche à droite, les gaz rares étant à droite.
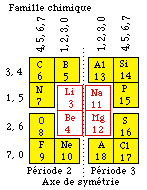
Fig. 249. Retournement de la figure précédente.
Retournements.
Le tableau précédent peut se retourner. Par exemple, les gaz rares en bas, comme dans la figure 249. L'axe de symétrie devient vertical.
Les périodes 4 et 5 en équerres et en tableau carré (blocs s et p).
Nous pouvons encore appliquer le processus précédent aux blocs s et p des périodes 4 et 5. Figure 250.
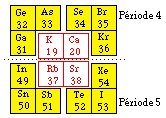
Fig. 250. Périodes 4 et 5 (blocs s et p) mises en tableau carré.
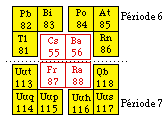
Fig. 251. Périodes 6 et 7 (blocs s et p) mises en tableau carré.
Les périodes 6 et 7 en équerres et en tableau carré (blocs s et p).
Nous pouvons enfin appliquer le processus précédent aux blocs s et p des périodes 6 et 7. Figure 251.
Les éléments réguliers en 3 tableaux carrés.
Périodicité bisoctave.
Les 3 tableaux carrés que nous venons d'obtenir, alignés horizontalement ou verticalment, renferment tous les éléments réguliers, au nombre de 48, jusqu'au québécium. Figures 252, 253.
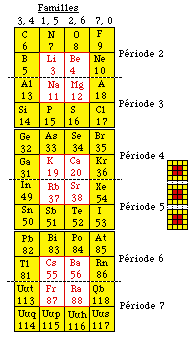
Fig. 252. Les 48 éléments réguliers des blocs s et p mis en 3 tableaux bisoctaves contenant des couronnes p . Alignement vertical. Progression des périodes de haut en bas, 2 familles chimiques dans chaque colonne, 4 dans chaque ligne avec répétitions.
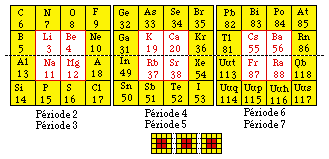
Fig. 253. Les 48 éléments réguliers des blocs s et p mis en 3 tableaux bisoctaves. Alignement horizntal. 4 familes chimiques dans chaque rangée avec répétition.

Fig. 254. Tableau Mendeleev-Seaborg (d'après la figure 230, avec marquage des blocs de cases).
Les périodes 4 à 7, les blocs d et f des éléments de transition mis en couronnes.
Nous pratiquons maintenant pliage et collage sur les éléments de transition formant les blocs d et f des périodes 4, 5, 6 et 7. Ces éléments sont au nombre de 56 jusqu'au québécium dans le tableau de Mendeleev. Figure 254.
À partir des 4 blocs d, nous obtenons des équerres qui s'associent en 2 couronnes pour les périodes 4, 5, 6 et 7. On reconnaît facilement dans ces couronnes les familles des scandides et de la mine de fer ou VIIIA et les groupes VIA et VIIA repérés dans le tableau de Parenteau figure 228. Figures 255 à 258.
À partir des 2 blocs f, nous obtenons une unique couronne pour les périodes 6 et 7. Elle est entièrement formée de deux familles, les lanthanides et les actinides. Figures 259, 260.
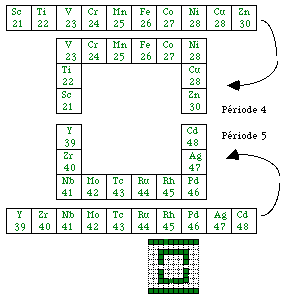
Fig. 255. Mise en équerres des éléments d des périodes 4 et 5.
Les 2 couronnes d et la couronne f constituent des circuits fermés. L'existence de ces nouvelles périodicités dépend chaque fois du groupement de 2 périodes traditionnelles : périodes 4 et 5, 6 et 7 pour les couronnes d, périodes 6 et 7 pour la couronne f.
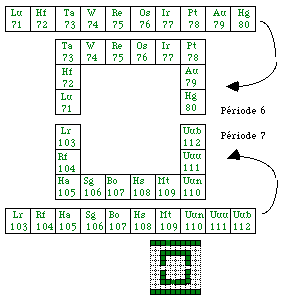
Fig. 256. Mise en équerres des éléments d des périodes 6 et 7.
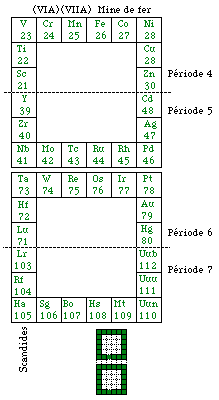
Fig. 257. Les 40 éléments des blocs d mis en 2 couronnes, alignement vertical. Familles.

Fig. 258. Les 40 éléments des blocs d mis en 2 couronnes. Alignement horizontal. Familles.

Fig. 259. Mise en équerres des éléments f des périodes 6 et 7.
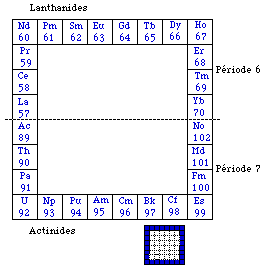
Fig. 260. Les 28 éléments f mis dans une unique couronne. Familles des lanthanides et des actinides.
Équerres et couronnes des éléments des blocs s.
Nous avons glissé sur le sujet des éléments des blocs s, présents à l'intérieur des 3 couronnes p des figures 252 et 253. Le groupement dessinsnt un carré de 4 cases s ne délimite pas d'espace central vide. Nous conviendrons nénmoins de le désigner comme une couronne avec espace central nul, pour la commodité du langage et par extrapolation à partir des couronnes plus grandes f, d et p, qui enferment respectivement un espace central de 36, 16 et 4 cases.
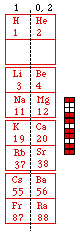
Fig. 261. Les 14 éléments s mis en 4 couronnes de 4 cases. Alignement vertical. Les familles .
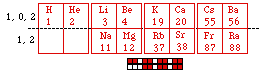
Fig. 262. Les 14 éléments s mis en 4 couronnes de 4 cases. Alignement horizontal. Les familles.
Il nous faut aussi envisager le cas du bloc s des 2 éléments mis à part formant la période 1, soit H et He. Par extrapolation à partir des couronnes formées dans les périodes suivantes, nous conviendrons que les 2 cases de ces éléments se logeront dans un carré de 4 cases, laissant 2 cases vides. Pure convention, qui laisse ouverte la question : pourquoi 2 cases vides?
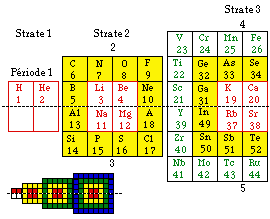
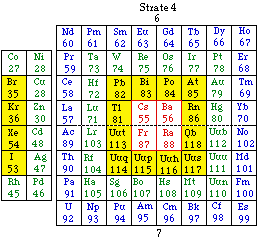
Fig. 263. Tableau des éléments dans le système du québécium, obtenu par pliage et collage. Tableau No 1.
Nous avons donc 4 couronnes de 4 cases, issues des périodes 1 à 7. Figures 261, 262.
Nous attribuons à l'hydrogène la famille 1.
Tout en rappelant la réserve pour la couronne H, He, nous notons que chacune de ces couronnes constitue un circuit fermé doué de périodicité.
Couronnes et équerres.
Pour la commodité du langage et des
concepts, nous conviendrons que la couronne de 4 cases contient 4 équerres d'une case. Ainsi, toutes les couronnes décrites sont formées de 4 équerres sauf celle de la période 1 qui est incomplète et n'en a que 2. Nous avons décrit ci-dessus un total de 10 couronnes soit 38 équerres.10 couronnes, 38 équerres, 118 éléments.
Ces 10 couronnes peuvent s'associer par emboîtements. Les 4 couronnes s s'augmentent de couronnes p, d et f dans l'ordre. Le résultat est un enchaînement répondant aux strates 1, 2, 3 et 4 entièrement occupées sauf 2 cases dans la strate 1. Voici donc un tableau des éléments, auquel nous sommes parvenus par pliage et collage d'un tableau de Mendeleev où apparaisent les blocs s, p, d et f.
Il répond au système du québécium décrit au chapitre 1. Figure 263.
Tableau original No 1.
C'est notre tableau original des éléments No 1 dans le système du québécium. On y reconnaît 118 éléments, 4 strates, 7 périodes, chacune comprise entièrement au nord ou au sud de l'axe de symétrie horizontal. Il présente un pairage constant des éléments comparables alcalins, alcalino-terreux et gaz rares, symériquement placés de part et d'autre de l'axe de symétrie . Les gaz rares se trouvent à la droite de chaque strate.
Au point de vue de la commodité du repérage, son plus grand mérite est probablement d'attribuer une place logique et condensée aux éléments de transition. Le repérage des lanthanides et des actinides est particulièrement facile puîsqu'ils occupemt à eux seuls la couronne f externe de la strate 4.
Cela réclame cependant que ces familles soient limitées l'une et l'autre aux 14 éléments du bloc f.
Les éléments appartenant à ces familles ont posé des problèmes d'insertion dans le tableau au fur et à mesure qu'ils étaient réalisés. Leur insertion exacte dans notre tableau No 1 à la couronne f de la strate 4 est une recommandation du système du québécium dan son ensemble avec ses autres couronnes et ses autres strates.
Les 2 cases vides.
Seulement 2 cases vides sur 120, dans la strate 1, c'est un progrès sur le tableau rectangulaire de Mendeleev présentant 106 cases vides sur 224. Cependant, si le système du québécium est fondé, on peut penser qu'il ne devrait y avoir aucune case vide.
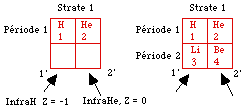
Fig. 264. Les cases vides . Des atomes infra. Des périodes remaniées.
Le problème ressemble à celui envisagé par Francis Perrin : devrait-on ajouter une case au dessus de celle de l'hydrogène pour le neutron? Voyez son tableau figure 231. Sa réponse a été négative, appeler le neutron une espèce chimique lui paraissant un peu abusif.
Voici 2 solutions possibles. Les cases vides sont 1' et 2'. Figure 264.
L'Infra-Hélium. Une solution se présente, basée sur la théorie des liaisons électrovalentes. Lorsqu'un alcalin s'unit à un halogène, il perd un électron et devient un ion positif ayant la structure électronique du gaz rare inférieur. Ainsi, le sodium devient semblable au néon, le lithium, à l'hélium. Le sodium devient un argonoïde, le lithium devient un hélioïde. Dans la formule ci-dessous, les nombres sont ceux des électrons attachés au noyau.
Na11+Cl17 = Na10++Cl18- = Neoïde10+Aoïde18
Li3+F9 = Li2++F10- = Heoïde2+Neoïde10
Remplaçons maintenant l'alcalin par l'hydrogène. De quel élément l'ion positif de l'hydrogène, c'est-à-dire le proton, est-il l'oïde, à quel gaz rare ressemble sa structure électronique? On est obligé de dire que ce gaz rare imaginaire, ne contenant aucun électron, a le numéro atomique Z = 0 et qu'il est l'homologue inférieur de l'hélium.
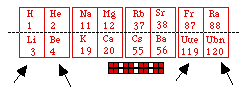
Fig. 265. Pour remédier aux cases vides. Les couronnes s remaniées.
Appelons le InfraHe, dans une création conceptuelle parallèle à celle de ÉkaAl de Mendeleev pour une case vide, qui a conduit à la découverte du gallium Ga = 31.
H1+Cl17 = H0+ +Cl18- = InfraHeoïde0+Aoïde18
On a donc écrit InfraHe Z = 0 dans la case 2'. Poursuivant notre effort imaginatif, on a écrit InfraH pour infra-hydrogène dans la case 1' et il faut bien lui assigner un numéro atomique Z = -1.
Ces atomes imaginés seraient distincts du neutron, qui est instable, et de l'antiproton, qui réagit instantanément avec les noyaux ordinaires.
Voilà un grand effort imaginatif, d'apparence artificielle.
Des périodes remaniées. Une autre solution existe, mais elle nécessite un remaniement de l'organisation traditionnelle des périodes.
Écrivons simplement Li3 dans la case 1' et Be4 dans la case 2'. Figure 264. Les 4 cases de la strate 1 sont remplies.
Cela entraîne un suivi. On ne peut inscrire Li et Be 2 fois dans le tableau. On les retire des places qu'ils occupent dans le tableau No 1 et on y écrit Na11 et Mg12.
Puis il faut courir en déplaçant tous les autres alcalins. Le résultat limité aux éléments s comme les montre la figure 262 apparaît figure 265. Sauf H et He, tous les éléments ont changé de place. Li et Be figurent à l'extrême gauche, et il faut bien inscrire un nouvel alcalin et un nouvel alcalino-terreux, non encore découverts, dans les cases qui autrement resteraient vides, à l'extrême droite, soit 118 Uue et 120 Ubn.

Fig. 266. Les 16 éléments s du tableau No 2 mis en 4 couronnes de 4 cases. Alignement vertical. Les familles. He est placé dans la même famille que les alcalino-terreux.
L'intervention de ces 2 éléments s'accorde mieux avec les usages admis que l'intervention des infra-éléments ci-dessus.
Les 4 couronnes s du tableau No 1 doivent alors être changées. Figure 266.
Cela nous conduit au tableau No 2. Figure 267.
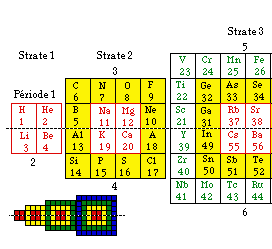
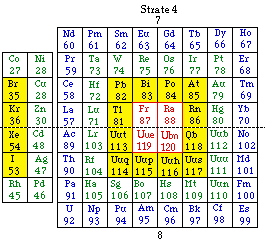
Fig. 267. Tableau No 2. 120 éléments, 8 périodes.
Tableau No 2.
120 éléments, 8 périodes, 4 strates.
Le nouveau tableau apporte immédiatement un remède à l'isolement de la période 1 de Mendeleev : la strate 1 renferme 2 périodes dont une nouvelle, voici leur composition :
...........
H1 et He2,...........
Li3 et Be4.La période 2 de Mendeleev est brisée. Elle a perdu Li et Be au profit de la période 2 nouvelle. Elle fournit 6 éléments à la période 3 nouvelle.
La période 3 nouvelle a 8 éléments et les 8 familles reconnues, mais l'alcalin et l'alcalino-terreux qu'elle renferme ne sont pas Li3 et Be4 mais plutôt Na11 et Ca12, empruntés à la période 4 de Mendeleev et placés à la fin de la période plutôt qu'à son début. Voici la période 3 nouvelle.
B5
......C6......N7......O8......F9......Ne10......Na11......Mg12Et ainsi de suite. Le tableau No 2 et le tableau No 1 ne diffèrent d'organisation que dans les couronnes s et de contenu que par l'addition des éléments 119 et 120 .
On montre les familles des couronnes s. Figure 266
Aux numéros atomiques Z croissants, les règles suivantes se vérifient :
un gaz rare est un élément suivi des éléments d'un bloc s;
toute période se termine par des éléments d'un bloc s.
De la sorte, la période 1 a un gaz rare et la période 2 n'a pas de gaz rare mais se termine par Be et il y a 8 périodes se présentant par paires d'égales longueurs, chaque paire constituant une strate. Figure 268 et Tableau 63.
Tableau 60 Contenu du tableau No 2.
Figure 267.
Strate 1. Périodes 1 et 2 de 2 éléments. Total 4 cases.
Strate 2. Périodes 3 et 4 de 8 éléments. Total 16 cases.
Strate 3. Périodes 5 et 6 de 18 éléments. Total 36 cases.
Strate 4. Périodes 7 et 8 de 32 éléments. Total 64 cases.
Total 120 cases.
Le nouveau tableau résout une question autement d'apparence insoluble. Où faut-il placer, dans la classification, les éléments mis à part que sont H et He? La réponse est naturelle : H au dessus de Li, He au dessus de Be. L'inertie chimique remarquable de He découle de la règle énoncée ci-dessus, savoir, d'avoir des éléments du bloc s à sa suite. De tels éléments sont inexistants à la suite de Be.
Le tableau No 2 est remarquablement symétrique quant à la répartition des cases des différents blocs. Dans l'ensemble, il a un axe de symétrie horizontal, les cases d'une période répondant aux cases d'une autre période; à l'intérieur de chaque strate, il y a un axe symétrie vertical pour les cases d'une même période.
Le tableau No 1 a les mêmes symétries sauf dans la strate 1 où fait défaut la symétrie par rapport à l'axe horizontal.
Dans le tableau No 2, le périodes impaires sont au nord de l'axe, les périodes paires au sud.
Un bilan chimique.
On voit que le tableau No 2 apporte sans effort une réponse aux difficultés de la classification à ses deux bouts : comment disposer les éléments, si peu nombreux, de la 1re période et ceux, nombreux au point d'encombrer, des deux dernières.
Le pairage des périodes
Pliage et collage tels que décrits avec pour résultat l'occupation exacte de la grille du système du québécium seraient impossibles sans le pairage en longueur des périodes de Mendeleev 2 et 3, 4 et 5, 6 et 7. Ce pairage, que la théorie quantique est incapable de justifier, trouverait une explication dans les exigences de symétrie que représente la géométrie du système du québécium.
8 périodes, tableau de Mendeleev.
La répartition en 8 périodes, 4 strates du tableau No 2 peut se transporter dans une grille de Mendeleev rectangulaire 8X32, une ligne par période. Comparé au tableau traditionnel, ce tableau est un gain en régularité, montrant 4 groupes de périodes pairées. Il est encombrant, mesurant 256 cases au total, dont 136 inocupées.
Le présent auteur a cru découvrir cette répartition en tableau de Mendeleev, découlant de son tableau No 2 et il l'a annoncé lors d'un colloque en France en 2001. Il a reconnu depuis ce temps qu'il avait été précédé par Tarantola en 1970. Celui-ci d'ailleurs a reconnu qu'il avait été précédé à son tour par Janet en 1929. Le travail de Janet est peu connu du public scientifique. Il y a là une intéressante question historique à élucider. Figures 232, 268.
Les tableaux No 1 et No 2 sont des contributions originales du présent auteur. Ils ajoutent au bien-fondé du tableau du type Janet.
Les 18 groupes de l'IUPAC.
En 1989, l'IUPAC a émis des recommandations. Délaissant le système de 8 groupes divisés en sous-groupes, le tableau de Mendeleev devra contenir 18 groupes (18 colonnes), de 1 pour les alcalins à 18 pour les gaz rares, les éléments du bloc d occupant les colonnes de 3 à 12. Les blocs f des Lanthanides et Actinides forment des groupes représentés en surplus. Dans le tableau No 2, la correspondance avec les cases de nos couronnes est facile à apercevoir. Dans chaque strate après la première, nos cases se présentent par paires symétriques de même numéro de groupe. Les blocs f se placent en une couronne. Figures 269 à 272.
http://fr.encyclopedia.yahoo.com/articles/do/do_4196_p0.html http://www.techniques-ingenieur.fr/affichage/dispIntro.asp?nGcmid=K100
Le pairage des périodes.
Pliage et collage tels que décrits avec pour résultat l'occupation exacte de la grille du système du québécium seraient impossibles sans le pairage en longueur des périodes de Mendeleev 2 et 3, 4 et 5, 6 et 7. Ce pairage, que la théorie quantique est incapable de justifier, trouverait une explication dans les exigences de symétrie que représente la géométrie du système du québécium.
Après pliage et collage vient vêlage.
Pour conclure ce chapitre : pliage et collage, c'est-à-dire simples transpositions géométriques, suffisent pour démontrer, quant à l'organisation des blocs d'éléments, l'équivalence du tableau de Mendeleev et des tableaux du système du québécium.
Au chapitre suivant, nous poursuivons l'étude de tableaux originaux dans le système du québécium en faisant appel au vêlage.

Fig. 268. Cette version du tableau de Mendeleev, équivalente à celle proposée initialement par Janet, découle naturellement de notre tableau No 2 transposé dans une grille rectangulaire 8X32. http://www.er.uqam.ca/nobel/c3410/SymQbNouResACFAS71.html
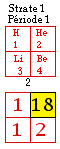
Fig. 269. IUPAC. Correspondance entre les groupes 1 à 18 de l'IUPAC 1989 et les cases de la strate 1 de notre tableau No 2.
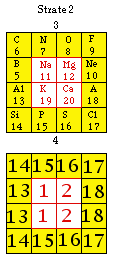
Fig. 270. IUPAC. Correspondance entre les groupes 1 à 18 de l'IUPAC 1989 et les cases de la strate 2 de notre tableau No 2. Symétrie nord sud.
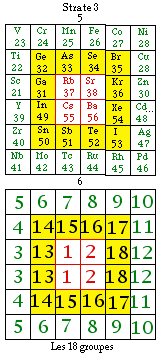
Fig. 271. IUPAC. Comme la figure précédente, strate 3. Seule parmi les 4 strates, la strate 3 renferme précisément 18 groupes.
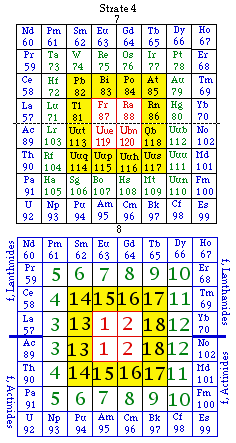
Fig. 272. IUPAC. Comme la figure précédente, strate 4. Addition naturelle des blocs f des Lanthanides et des Actinides sous la forme d'une couronne.
![]()
QbSyst2e.20.html
Système du Québécium
Suivant QbSyst2e.21.html
Précédent
QbSyst2e.19.htmlDébut QbSyst2e.1.html