3DLesTableaux

http://www.lisulf.quebec/quebecium.htm

Système du Québécium

Les tableaux périodiques 3D depuis 1862 et de nos jours.

Pierre Demers

EAPD

Traduction interdite

28XI–7XII2010

Résumé. HISTORIQUE. On trouve près de 50 tableaux périodiques 3D depuis le 1er, en 1862, l'hélice de Chancourtois qui précéda le tableau 2D de Mendeleev. Tous marquent les périodicités chimiques et les plus récents se soucient en outre de nombres quantiques, géométries et symétries. Je signale en 1979, les revendications de Jess Tauber avec son tétraèdre en instance d'être breveté et la réalisation d'un arbre des éléments par Fernando Dufour le Montréalais; en 2007 Valéry Tsimmermann et en 2008 Richard Kingstone le Néo-Brunswickois. INNOVATIONS. Mes travaux originaux depuis 1995 suggèrent une géométrie quantique basée sur le nombre magique 4, ajoutant à la mécanique quantique connue, apportant une sorte d'unification entre la théorie de la matière inerte et celle de la matière vivante. Ce dernier sujet a été illustré en 2010 par la synthèse de la vie par Craig Venter et par la création d’un périodique sur la Chimie Systémique. Voyez mon site, je présenterai plus de 15 tableaux 3D dont quelques uns inédits. D’après Réf.1.

Le répertoire.

La référence 2 donne une liste étendue des tableaux périodiques des éléments TPÉ classsés par année de publication et accompagnés de commentaires. Une section est intitulée Tableaux spiralés et une autre, Tableaux 3D. Voici un extrait en français de la section Tableaux 3D.

Une liste d’après Réf.2.

1•1862 Chancourtois, Vis tellurique,

2•1872 Meyer, Spirale

3•1881 Spring, Hélice

4•1898 Crooke, Fil de fer

5•1911 Emerson, Hélice

6•1911 Soddy

7•1916 Harkins et Hall

8•1920 Schaltenbrand

9•1920 Kohlweiler, Système

10•1920 Schaltenbrand

1925 Courtines

1925 Friend

1928 Janet, Tube spirale

1928 Janet, Hélicodal

15•1928 Janet, Lemniscate

1934 Romanoff

1943 Finke

1947 Stedman, Conique

1949 Wringley, Laminaire

20•1951 Chicago, Musée de la Science et de l’Industrie

1951 Edgar Longman, Murale Festival 1951 Exposition Science Britannique

1960 Sphérique

1965 Alexander, bureautique

1974 Mazurs, en bois

25•1974 Mazurs, Analyse

1974 Mazurs, Version du Lemniscate de Janet

1980 Table Ronde

1983 Chimistes du Ciment, Cubique

1983 Pyramide

30•1995 Fractale, Fraundorf

http://www.umsl.edu/~fraundorfp/nanowrld/newlive/ptable3d.html

1996 FernandoDufour, Arbre

2003 Cylindre et Bombement

2003 Élephantesque

2003 Des Électronégativités

35•2004 Rafael Poza

2005 Pyramide

2006 Alternative Wikipédia

2006 Spiralé

2007 Tsimmerman Tétraèdre ADOMAH

40•2007 Deuxième Vie

2007 Circulaire Wikipédia

2007 Gyroscopique

2008 Empilement Kingstone

2008 Rafael Poza, Magnetosphere

45•2008 Tomás A. Carroll, Sphérique et Poupée Russe

2009 Steve Jensen, Infini

2009 Graphique

2009 Nasco, Jeu de Balle

49•2009 Fleur Med Russe

NB. En 1930 Janet. Un modèle en couches non 3D mais a formulé en 1930 la règle n+l habituellement dite de Madelung, 6 ans avant Madelung.

Additions, auteurs divers.

Il faudrait ajouter. 50•1979-2010 Jess Tauber. Voyez Réf. 5. Selon sa correspondance en 2010, Jess Tauber soutient qu’il a présenté en 1979 à un auditoire de l’ACS (Société Américaine de Chimie) un Tableau 3D des éléments chimiques en tétraèdre de boules.

À propos de 39 ci-dessus Tsimmerman Tétraèdre ADOMAH, voyez Réf. 6.

À propos de ci-dessus 43 Kingstone Empilement, voyez Réf. 7

Tableaux 3D originaux de l’auteur Pierre Demers.

Voici des tableaux périodiques 3D originaux dont l’auteur est Pierre Demers, numérotés à partir de D1.

Pour visionner D1 à D12, déclenchez Réf. 8. et cherchez la figure.

Qb1 Fig. 1. Tableau 3D/01. Tableau en relief.

Qb 2 Fig. 2. Tableau 3D/02. Tableau en pyramide à base carrée.

Qb 3 Fig.3. Tableau 3D/03. Tableau en pyramide tétraédrique de 120 boules.

Qb 4 Fig . 4. Tableau 3D/04. Tableau en pyramide tétraédrique de 120 rhombododécaèdres. - Fragment.

Qb 5 Fig 5. Tableau 3D/05. Quatre pyramides quadrangulaires.

Qb 6 Fig. 6. Tableau 3D/06. Étoile à 4 branches de 30 boules chacune.

Qb 7 Fig. 8. Tableau 3D//01. Tableau en tétraèdre coiffé.

Qb 8 Fig. 9. Tableau 3D//02. Tableau 3D en tétrades octaèdres quart d'ellipse.

Qb 9 Fig. 10. Tableau 3D//03. Modification de la figure précédente.

Qb 10 Fig. 11. Tableau 3D//04. Tableau 3D en tétracônes.

Qb 11 Fig. 13. Tableau 3D//05. Le tableau platonicien. Un solide représente non un élément mais plusieurs.

Qb 12 Fig. 14. Tableau 3D//06. Avec déploiement et clé de lecture.

Pour visionner D13 et D14, déclenchez Réf. 6 et cherchez la figure.

Qb 13 Fig. 10 de Réf. 6

D14 Fig. 4, Fig. 5, Tétraèdre, sur ses 4 faces, 1995,6

Innovations, le tétraèdre tronqué.

Voici d’autres tableaux 3D originaux de l’auteur. Je reprends D8 et je cherche à optimiser l’agencement pyramidal de formes en plusieurs exemplaires du tétraèdre régulier et de ses troncatures, au nombre de 1, 2, 3 ou 4.

Le tétraèdre régulier de Platon se prête à des troncatures sommitales au nombre de 1, 2, 3 ou 4, qui augmentent le nombre de ses faces d’autant. Chaque face ajoutée est un triangle, et finalement il reste 4 faces hexagones et 4 faces triangles équilatéraux, hexagones et triangles ayant l’arête quart de celle du tétraèdre original. Voici la liste des 5 variétés à envisager.

Variété 0...0 troncature........ tétraèdre régulier de Platon

Variété 1...1 troncature........ pentaèdre

Variété 2...2 troncatures....... hexaèdre

Variété 3...3 troncatures....... heptaèdre

Variété 4...4 troncatures....... octaèdre tétraèdre tronqué d’Archimède

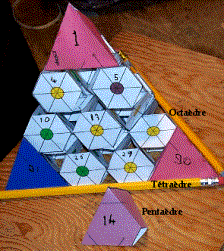
Fig. 1. Pyramide de tétraèdres tronqués d’un tableau quart d’ellipse 3D en 30 tétraèdres de tétrades numérotées de 1 à 30. On imagine le nom d’un élément inscrit sur chacune des 4 faces hexagonales de chaque tétrade. Voyez ces noms dans la figure suivante Fig. 2.

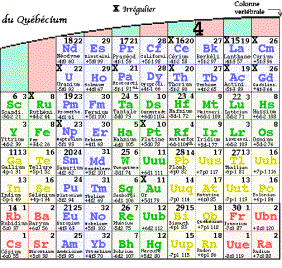
Fig. 2. Le tableau quart d’ellipse 2D en 30 tétrades, numéros de 1 à 30 (1H, 2B, 3C,... 28Pb, 29Bi, 30Fr). Les 4 strates 1234. La structure d’une tétrade est détaillée dans l’encart. À l’intérieur d’une strate, le moment cinétique orbital l reste constant, selon la couleur. Il y a un jeu touchant les spins s et le nombre quantique principal n. gqafig15,54aquartd.gif, gqafig15,54bquartd.gif (JdBquartdell.gif)

J’ajoute ici l’hexaèdre et l’heptaèdre aux formes désignées Fig. 10 dans Réf. 8. reproduite dans la présente Fig. 1. Ces formes aux faces colorées aux 4 couleurs sont douées de chiralités ou d’énantiomorphismes, propriétés étudiées ailleurs. Réf.10. La compositon des strates successives apparaît Fig. 2.

Je cherche ainsi les variantes de Fig. 1 qui pourraient présenter un intérêt au point de vue d’une théorie des symétries.

Hypothèses. Je suppose 4 strates autonomes chacune, càd que chacune occupe son espace propre au complet tout en lui restant confinée et sans déborder sur une strate voisine. On se donne comme objectif de confectionner une pyramide tétraédrique massive sans espace vide, ce qui n’est pas réalisé Fig. 1. La question n’est pas de rendre le tableau commode de consultation, mais de comprendre les symétries de l’occupation spatiale.

Voici le patron universel permettant d’obtenir par découpage, pliage et collage chaque variété ci-dessus.

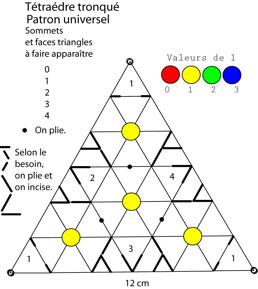
Fig. 3. Patron universel des tétraèdres tronqués. Tron012347XII2010.png

Discussion.

Strate 1. La strate 1 apparaît immédiatement comme se distinguant des 3 suivantes, puisqu’elle et elle seule consiste naturellemment d’un tétraèdre platonique. Elle et elle seule peut se concevoir en l’absence des 3 suivantes, car un atome stable z>4 ne peut exister qu’en présence des atomes z’<4 donc de la strate 1. Fig. 4

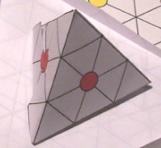
Fig. 4. Strate 1. Tétraèdre. TetraStrate16XII2010.png

Il nous faut isoler les représentations de chacune de 3 strates suivantes 2, 3, 4 pour les apercevoir au complet. Chacune doit se limiter à occuper un tronc de pyramide limité par deux triangles plans haut et bas distants de la hauteur d’un tétraèdre tronqué. Par suite, elles ne peuvent renfermer aucune tétraèdre de Platon.

L’espace propre d’une strate après la 1^re est un tronc de tétraèdre limité par 2 parois triangles plans inégaux parallèles. Une galette. (Qui donc a dit : « S’ils n’ont pas de pain, qu’ils mangent de la galette » ?)

Strate 2. Pour la commodité de la discussion, isolons la strate 2. Fig. 5.

Fig. 5. Strate 2. La variété 0 tétraèdre de Platon est exclue. Les tétrades sont ansi: 2R, 3J en haut, 4J en bas, 5J au centre. On ne peut pas avoir la variété 5 octaèdre partout, mais elle obligatoire pour la position centrale tétraèdre 5. Je choisis hexaèdre pour la tétrade 3, alors 4 est pentaèdre. D’autres options sont possibles. Strate27XII2010.png

Fig. 6. Qb15 Tableau 3D en tétraédres tronqués (partiel). Ce tableau 3D résulte des Figs 4 et 5 réunies et comprend les éléments z de 1 à 20. On aperçoit, au moins partiellement, les tétraèdres de chacune des 5 tétrades de 1 à 5. Qb157XII2010.png

En réunissant les figures 4 et 5, je présente un nouveau tableau 3D tétraédrique partiel comprenant les 20 élémnts z = 1 à 20 des 2 1res strates. Ce tableau est original et je le désigne temporairement comme Qb15. Fig 6.

Conclusions.

La dernière figure montre un tableau 3D tétraédrique original Qb15. Je me propose, dans une publication distincte, de poursuivre les réflexions sur les strates 1 et 2 et de les amorcer pour les strates 3 et 4. – Au total, voilà donc 65 tableaux 3D des éléments chimiques répertoriés, 50 d’autres auteurs et 15 du présent auteur.

Références

Réf.1. Pierre Demers 2010, EAPD, Système du Québécium. Tableaux périodiques 3D des éléments chimiques. Bref historique depuis 1862 et innovations récentes. Soumis à l’ACFAS pour le 79^e congrès Univ. de Sherbrooke, proposition 4608.

Réf.2. Mark B. Leach 2010, Liste, en anglais, des tableaux périodiques des éléments avec lien et commentaires sur chaque entrée.

http://www.meta-synthesis.com/webbook/35_pt/pt_database.php

Ne mentionne aucune de mes publications, qui remontent à 1995, et qui sont accessibles sur la toile (depuis au moins 2001). Étonnant dans un pays à l’avant-garde de l’information de tout genre extra-rapide et universelle! Entre autres Réf. 8: http://www.lisulf.quebec/Qb1995,6.html

Réf. 3. Pierre Demers 2010, EAPD, Système du Québécium. Site. http://www.lisulf.quebec/quebecium.htm,

Réf. 4. Günter von Kiedrowski et al. 52010, Journal of Systems Chemistry., http://www.jsystchem.com/content/1/1/1

Réf. 5. Jess Tauber et Pierre Demers 2010, Correspondance. Courriels.

Voici une de ses références http://www.sciscoop.com/2005-7-20-10594-0329.html Et un passage d’un courriel reçu de Jess Tauber en mai 2010. («Veuillez prendre note que j’ai découvert la relation avec le tétraèdre déjà en 1979,... ») « You should remember that I discovered the tetrahedral relation back in 1979,.. » Et d’un autre que je lui adressais en avril 2010. « Encore moi. Essayez de trouver vos vieux documents, vos vieux souvenirs, les auditeurs JACS à la réunion locale en 1979, il y a sans doute des des survivants. Lesquels? ACS (SociétéAméricaine de Chimie). “À chacun ce qui lui appartient, sa propriété intellectuelle et autre! La vôtre, la mienne. Bonne chance. Donnez-moi des nouvelles. Et vive le Québec enchaîné. Amical. Pierre Demers Québécium LISULF il est jeudi in albis 8 IV 2010.”

Réf. 6 Système du Québécium. Le tétraédre dans la classification des éléments chimiques. Une note historique. Une version nouvelle du tableau tétraédrique des éléments. Pierre Demers. EAPD. Traduction interdite.12-26I2010.

Extrait : “La publication par Tsimmermann d’un tableau tétraédrique des éléments chimiques daté de 2007 me suggère de rédiger la présente note d’antériorité pour faire mieux connaître mes propres travaux originaux à ce sujet, qui remontent à 1996. J’ajoute la présentation d’une version originale d’un tel tableau. La méthodologie en est une de recherche de symétrie dans le cadre du système du québécium.»

Réf. 7. Richard Kingstone et Pierre Demers 2010, 12IX. Correspondance courriel.

Extrait.” RKingstone@solaris-mci.com, (helene_1@sympatico.ca), Bonjour Pierre. Oui, je serai heureux insérer un lien vers votre site dans ma page Web. Le lien doit être; <http://www.lisulf.quebec/quebecium.htm>http://www.lisulf.quebec/quebecium.htm>

Réf. 8. Pierre Demers 2008, Tableaux 3D Système du Québécium. Nouveaux tableaux 3D des éléments chimiques. Traduction interdite. 17XI2008.

Réf. 9. Pierre Demers 1995,6, Centre Québécois de la Couleur 1995, Nouveau système périodique des éléments. Treillis et couplage SS. Affinités biologiques. I Présentations 3D. Structure hélicoïdale du système des éléments 40. Traduction interdite.

Réf.10 SSVolCompl2ncell.htm

-30-