Une suite aux vidos de Patrick Callet.
Systme
du Qubcium.
Les
affichages du tableau priodique des lments.
Ë
la recherche d'un affichage symtrique
bas
sur les formules lectroniques.
Dans
le systme du Qubcium.
Pierre
Demers.
Le
14 fvrier 2015. Modifi 015-05-05
Traduction
interdite.
Une suite aux vidos de Patrick Callet.
Patrick Callet a ralis avec moi 2 vidos enregistrs en 2004 et mis en forme en 2014 et 2015. En ayant pris connaissance, voici un texte qui pourrait servir leur mise jour en fvrier 2015. Rfs 3, 4.
La liste des lments chimiques.
Voici la formule lectronique du Jantium 120Ja, qui contient celles
des 120 lments chimiques que je considre. Fig. 1
Fig. 1. Tableau 1. Formule lectronique du jantium.
Je dsigne l'lment de numro atomique z par
son caractre propre.
Voici les caractres des atomes ou lments
des numros atomiques z de 1 120.
Un atome renferme z protons et z lectrons.
La formule d'un lment comprend son caractre propre et celui de
tous les lments prcdents jusqu' z = 1. Ainsi, la formule du jantium
comprend tous les lments.
Les numros atomiques z vont de 1 120.
Le 1er chiffre va de 1 8, il est le quantum
principal. La lettre s, p,
d ou f,
dsigne le quantum azimutal 0, 1, 2 ou 3 et la couleur correspondante est R, J, V ou B.
Isol, le signe - ou + est le spin de
l'lectron qui contribue dfinir le caractre propre.
Numro z Caractre
|
1 10 |
1s0- |
1s0+ |
2s0- |
2s0+ |
2p-1- |
2p0- |
2p1- |
2p-1+ |
2p0+ |
2p1+ |
|
|
11 20 |
3s0- |
3s0+ |
3p-1- |
3p0- |
3p1- |
3p-1+ |
3p0+ |
3p1+ |
4s0- |
4s0+ |
|
|
21 30 |
3d-2- |
3d-1- |
3d0- |
3d1- |
3d2- |
3d-2+ |
3d-1+ |
3d0+ |
3d1+ |
3d2+ |
|
|
31 40 |
4p-1- |
4p0- |
4p1- |
4p-1+ |
4p0+ |
4p1+ |
5s0- |
5s0+ |
4d-2- |
4d-1- |
|
|
41 50 |
4d0- |
4d1- |
4d2- |
4d-2+ |
4d-1+ |
4d0+ |
4d1+ |
4d2+ |
5p-1- |
5p0- |
|
|
51 60 |
5p1- |
5p-1+ |
5p0+ |
5p1+ |
6s0- |
6s0+ |
4f-3- |
4f-2- |
4f-1- |
4f0- |
|
|
61 70 |
4f1- |
4f2- |
4f3- |
4f-3+ |
4f-2+ |
4f-1+ |
4f0+ |
4f1+ |
4f2+ |
4f3+ |
|
|
71 80 |
5d-2- |
5d-1- |
5d0- |
5d1- |
5d2- |
5d-2+ |
5d-1+ |
5d0+ |
5d1+ |
5d2+ |
|
|
81 90 |
6p-1- |
6p0- |
6p1- |
6p-1+ |
6p0+ |
6p1+ |
7s0- |
7s0+ |
5f-3- |
5f-2- |
|
|
91 100 |
5f-1- |
5f0- |
5f1- |
5f2- |
5f3- |
5f-3+ |
5f-2+ |
5f-1+ |
5f0+ |
5f1+ |
|
|
101 110 |
5f2+ |
5f3+ |
6d-2- |
6d-1- |
6d0- |
6d1- |
6d2- |
6d-2+ |
6d-1+ |
6d0+ |
|
|
111 120 |
6d1+ |
6d2+ |
7p-1- |
7p0- |
7p1- |
7p-1+ |
7p0+ |
7p1+ |
8s0- |
8s0+ |
|
Je remarque dans Fig.
1, une sorte de priodicit: celle des 16 entres s, prsentes par paires 8
fois des intervalles croissants. J'arrte la liste sur z = 120 8s0+ un
alcalino-terreux, par analogie avec les priodes 7prcdentes.
Pourquoi arrter
z = 120 ni avant ni aprs? Rf. 10. 6IV2015
Conventions.
Je conviens de 120 lments, de 1H 120Ja. 120Ja est un lment spculatif,
Spculatif veut dire considr, indpendamment de son observation exprimentale. Ma liste contient 8 lments spculatifs. Rg. 5.
Je m'attache aux proprits lectroniques, or 1H et 2He sont des lments s en rouge, aussi bien que les alcalins et les alcalino-terreux reconnus. Je conviens de traiter 1H comme un alcalin, et 2He comme un alcalino-terreux, sans pour cela prtendre altrer leurs proprits chimiques. Je m'intresse aux les proprits lectroniques pour la prsente cl;assification.
La liste des 120 lments: voyez les Annexes 1 et 2 et le Tableau 1 Fig. 1.
I. Affichage unidimensionnel.
Un affichage possible est linaire sur une seule ligne, avec 120 entres. Vu sa longueur, il est impossible de le prsenter sur papier de format habituel sans alinas. Voici du moins son dbut et sa fin. Fig. 2.
1H 120Ja
Fig. 2. Un affichage unidimensionnel du tableau des lments. Sans interruptions. Sans alinas.
Si je laisse des espaces vides sans alinas, le rsultat est encore plus encombrant. Du moment o il y a des alinas, le rsultat est bidimensionnel.
Avec des alinas aux 10 entres, voyez Fig.1.
Passer au paragraphe suivant II.
On peut aussi afficher en corde linge ou en chapelet.
Il semble exister unanimit chez les auteurs sur le contenu de cette liste unidimensionnelle Fig. 1, affichage unidimensionnel. Il en est autrement des affichages bi- et tridimensionnels. Voici lplus bas l'affichage bidimensionnel que je propose dans le systme du qubcium.
Ibis. Affichage pseudo-bidimensionnel.
Des choix, un choix. L'affichage du tableau habituel de Mendeleev est bi-dimensionnel, on ne peut le nier. Il occupe en effet plusieurs ranges horizontales, avec de nombreuses cases restant vides.
Forme longue. Dans la forme longue, chacune de ses priodes occupe une range horizontale.
Forme brve. Dans sa forme brve, cela reste vrai pour les priodes prcdant l'avant-dernire
L'avant-dernire priode occupe 2 ranges, la 2e range comprenant exclusivement l5 lments f. Il en est de mme pour la dernire priode.
Du point de vue graphisme, le tableau exploite incompltement la bi-dimensionnalit qui est disponible. En effet, chacune de ses ranges contient des lments de spin - puis de spin +.: ainsi H et He ds la 1re range.
Suite dans Annexe 1.
II. Affichage bidimensionnel.
En 8 priodes. Un affichage bidimensionnel possible est un morcellement en 8 priodes dont on montre le dbut et la fin. La fin de chaque priode est un alcalino-terreux en rouge.
Les priodes se prsentent par paires d'gales longueurs. Il se trouve que les priodes se prsentent par paires d'gales longueurs. Dans le tableau de Mendeleev, ce rsultat n'apparat qu'aux priodes suivant la 2e. Dans les conventions que je choisis, cette observation s'applique aux 8 priodes. Fig. 2.
1H 2He
3Li 4Be
5B 12Mg
13Al 20Ca
21Sc 38Sr
39Y 56Ba
57La 88Ra
89Fr 120Ja
Fig. 3. Les 8 priodes. En supprimant les entres en italiques, elle se condense en 4 lignes, une par strate de 2 priodes gales. Les lignes successives ont 2, 2, 8, 8, 18,18, 32 et 32 lments
En supprimant les entres en italiques, il se condense en 4 lignes, une par strate de 2 priodes gales.
En 4 strates. J'appelle strate une paire de 2 priodes successives d'gales longueurs. Ayant supprim les entres en italiques dans Fig. 2, l'affichage se condense en 4 lignes, une par strate de 2 priodes d'gales longueurs. Fig. 4.
1H 4Be
5B 20Ca
21Sc 56Ba
57La 120Ja
Fig. 4. Dcoulant de Fig. 2, en supprimant les entres en italiques. Les 4 strates. Les lignes ont successivement 4, 16, 36 et 64 lments.
Les lignes ont successivement 4, 16, 36 et 64 lments. Ce sont les quadruples des carrs des 4
premiers entiers 1, 2, 3 et 4. La somme des ces carrs est 30. Ils
interviennent par leurs quadruples.
Nombre 4. Des nombres figurs.
Le nombre 4 se
prsente avec insistance! Et ce n'est qu'un commencement.
Je peux figurer ces
observations gomtriquement, par ce qu'on appelle des nombres figurs.
En nombres figurs 4, 16, 36 et 64. En voici une reprsentation, par des
carrelages de cases toutes semblables, chacune tant un carr de ct
arbitraire. Chaque carr a 4 cts. Je peux ainsi partir de 4 carrelages
identiques de 64 cases qui seront utilises incompltement sauf pour la strate
4. Figs 5 9.
.
. .
.
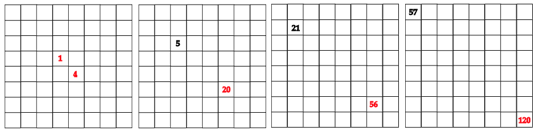
Fig. 5. Carrelages pour les 4 strates. . 4grilles64cases2015-02-10
à 17.26.51.png
.  .
.
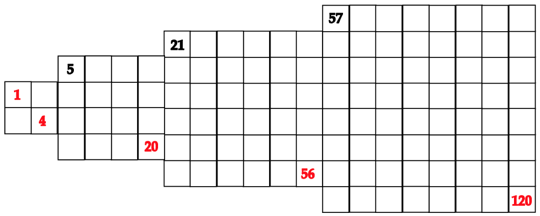
Fig. 6. Carrelages, avec indication des
limites des 4 strates. 4Grilles12342015-02-12 à 04.45.35
.  .
.
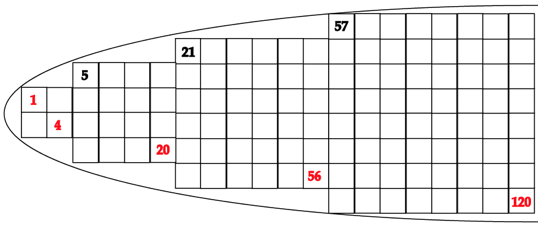
Fig. 7. Les 4 strates, aprs suppression des
cases superflues, rapprochements et changement d'chelle. Capture dÕécran
2015-02-11 à 14.09.35
.
 .
.
Fig. 8. Tableau en demi-ellipse. Les 4
strates jointives s'inscrivent sensiblement dans une demi-ellipse.
AvecDemi-ellipse 2015-02-11 à 00.52.25.png
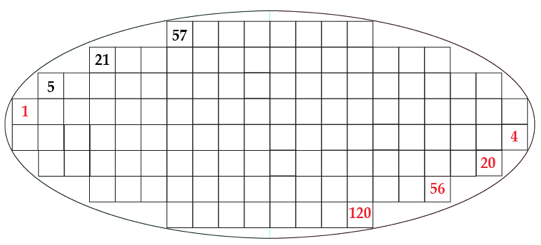
Tableau elliptique. Ë la condition de diviser les strates 1, 2
et 3, je peux arriver un tableau elliptique, la strate 4 restant inchange au
milieu. Je divise les strates, 1, 2 et 3 en moitis ouest et est. Fig. 9.
. ![]()
 .
.
Fig. 9. Tableau elliptique. Les strates 1, 2
et 3, ont t divises en moitis Ouest et Est.Ellipse2015-02-11 à
14.42.54.png
L'affectation des cases. Une recherche de
symtrie. Le tableau de Mendeleev contient des symtries imparfaites et j'y vois
une invitation tenter de faire mieux, en utilisant Figs 7, 8 et 9. Voici les
donnes.
Quant aux Figs 7 et 8,
leur aspect suggre de rechercher une symtrie par rapport une droite
diamtrale OE, cd une symtrie NS .
Les strates prises individuellement Fig. 7
sont des carrs, ce qui suggre de rechercher en plus des symtries par rapport
au point centre de figure, cd OE et NS.
Diviser selon le spin - ou +. En inspectant le Tableau 1 Fig. 1, je
reconnais que les spins sont rpartis en nombres gaux: 60 entres - et 60
entres +. J'en tire la suggestion de placer spins - l'Ouest et signes +
l'Eest. La 1re entre - est 1s0-l,
la 60e + entre + est 8s0+.
Diviser selon les blocs - ou +. En inspectant nouveau le Tableau 1 Fig. 1,
je remarque que les entres de signe - sont prsentes par blocs rassemblant
chacun un nombre impair d'entres: 1, 3, 5 ou 7. En nombres figurs, ces blocs
peuvent se figurer par des querres ayant deux bras de 0, 1, 2 ou 3 cases. Il
en est de mme quant aux blocs +.
Ë l'Annexe 3, voyez
ces querres, qui comprennent tous les 120 lments. Je compte 16 querres R,
12 querres J, 8 querres V et 4 querres B, soit 40 querres au total. Elles
s'assemblent sans faute comme une marquetterie, pour donner 16 quadrants dans
les 4 strates.
J'associe ces
querres selon des rgles qui se proposent. Chacune des strates est le lieu de
placements dans les cases selon des rotations dans le sens horaire, celui des
aiguilles de l'horloge et tantt dans le sens oppos.
. 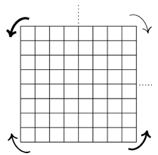 .
.
Fig. A3.
L'criture est anti-horloge aux quadrants NO et SE, horloge aux
quadrants SO et NE. flches.png
L'ordre du remplissage des quadrants est
selon l'paisseur des traits des flches.
Il commence dans le quadrant NO et se termine
dans le quadrant NE.
Voici le tableau
semi-elliptique des 120 lments, tous lments en place, un tableau
bidimensionnel. 12II2015.
. 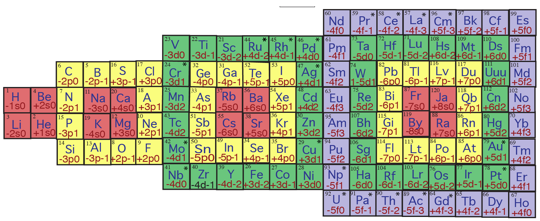 .
.
Fig. 10. Un tableau bidimensionnel des 120
lments en demi-ellipse. LaDemiEllipse2015-02-12 à 17.34.58.png
Dans ce tableau en
demi-ellipse, je remarque une symtrie d'ensemble binaire par rapport l'axe
horizontal. Ainsi Rh et Co, leurs caractres ont en commun d-1. Dans ce dit tableau
en demi-ellipse, il n'y a pas de symtrie d'ensemble par rapport un axe
vertical. Par contre, dans chaque strate, je remarque une symtrie quaternaire
par rapport un point central. Ainsi C, Si, Cl et F, leurs caractres ont en
commun p0. Il n'y a pas de point central dterminant d'une symtrie d'ensemble.
Mais je passe de Fig,10
Fig. 11 par des translations horizontales qui prservent les symtries par
rapport l'axe horizontal. En procdant de la sorte, j'ajoute, pour les cases
des strates 1, 2 et 3, des symtries par rapport l'axe vertical de
l'ensemble. Symtrie par rapport 2 axes croiss, cela revient une symtrie
par rapport au point de croisement.
. 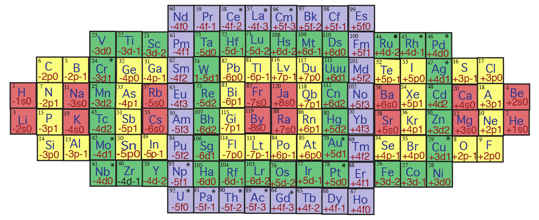 .
.
Fig. 11. Un tableau bidimensionnel des 120
lments en ellipse. EnEllipse2015-02-12 à 17.30.26.png00
Dans ce tableau en
ellipse, je remarque donc une symtrie gnrale par rapport un point central.
Ainsi C, Si, Cl et F, leurs caractres ont en commun p0. Le passage de tableau
en semi-ellipse tableau en ellipse a prserv les symries quaternaires, tout
en distanciant leurs participants des strates 1, 2 et 3 divises.
III. Affichage tridimensionnel.
En mousses.
Voici un essai datant de 1995 les lments R composent une colonne centrale haute de 4 strates; concentriquement alentour, les lments J composent une chemine haute de 3 strates, les lments V, une couronne haute de 2 strates, et les lments B, une couronne haute d'une seule strate. Cette maquette a servi lors du baptme du Qubcium en 1996, la marraine tait Mme Huguette Proulx-Arsenault, au cours d'un congrs de l'APSQ Hull. Rf. 4
. .
.
Fig. 12. Tableau 3D en mousses, je suppose
les cases cubiques individuelles de mme couleur soudes ensemble. Hauteur 4
cubes, largeur et longueur 8 cubes. Par des glissements, je peux isoler soit
les suites de l'une des 4 couleurs, soit les composantes de l'une des 4
strates.
En cubes de bois.
Voici les priodes
1, 2 et 3. Figs 13, 14.
. 13.  .
. .14
.14
Fig. 13, 14. Les priodes 1, 2, 3. Isoles;
superposes. 3Périodes2015-02-13 à 18.09.24.png
En ttradre de boules.
Je remplace les 120 cases carrs par des autant de boules sphriques. Je les superpose en 8 niveaux se groupant naturellement en 4 strates de 4, 16, 36 et 64 boules, rparties en 10 compartiments aux 4 couleurs R, J, V et B. Figs 15, 16.
.  .
.
Fig. 15. Ttradre autoportant de 120 boules, vers un tableau 3D des 120 lments. Tétra120Boules13II2025IMG_1559.jpg
.  .
.
Fig. 16. Comme Fig. 15, mais la tte en bas. Cette tte est l'atome 1H. Ceci pour rappeler la prsence de cet atome dans tous les atomes de la matire ordinaire. Noter la prsence apparente d'antigravit dans les ficelles qui pendent vers le haut de la figure! TétraBouleshautbasIMG_1559 .jpg
Voyez Rf. 4.
IV. Nombres magiques et universalit du systme du Qubcium.
Ë suivre. Rf. 6.
V. Envoi.
Le contexte des vnements
au Qubec en fvrier 2014 me suggre les prsentes observations. Je ne peux m'y
soustraire.
1.
"L'avenir de l'Observatoire astronomique de Mgantic est en
pril" ... "... il est
sauv!"
Ë ce sujet, les paroles du Recteur Breton
de l'UdeM.
"...les rseaux
internationaux de la recherche en astronomie et en arospatiale et contribue
repousser toujours plus loin nos connaissances sur lÕUnivers
pour toute personne qui sÕintresse la science au Canada. .
(Une pense pour le
Qubec?)
-LÕObservatoire du
Mont-Mgantic survivra pour au moins deux ans 11 fvrier 2015 20h52 |Mlanie Marquis - La Presse
canadienne | Canada
PiD. Mieux que rien?
Quelle piti que la science du Qubec soit une fois de plus la merci d'un
gouvernement qui ne veut pas de nous depuis 1982 et qui prend l'argent dans nos
poches pour le distribuer en son nom et perptuer son autorit illgitime.
Accepter le pain de la captivit?
Le
dput libral de Westmount–Ville-Marie au fdral, Marc Garneau, a
dnonc lÕidologie du gouvernement Harper en ce qui concerne le financement de
la recherche au Canada. Ç Ce
gouvernement a clairement donn le message, il y a quelques annes, quÕil
dsirait favoriser la recherche applique qui aboutit des dbouchs
commerciaux, plutt que la recherche fondamentale, comme lÕastronomie qui
accrot notre connaissance de lÕUnivers È,
Le Systme du Qubcium, lui
aussi, accrot notre connaissance de l'Univers, de sa matire et de sa vie.
2. Gilles Rhaume 1957-2015 est dcd le 8 fvrier
2015. Grand patriote et ami de la LISULF.
3. Patrick Callet, professeur l'cole Centrale de Paris, qui fut l'un des
confrenciers la Maison Duvernay le 8 novembre dernier, reoit une publicit
inattendue pour sa reconstruction virtuelle de l'Abbaye de Royaumont,
maintenant disparue, devenue un quartier de Cherbourg.
Rfs 7, 8 et 9.
Annexe 1.
Liste des lments et de leurs caractres selon z
le nombre d'lectrons.
La liste complte des caractres est galement la
formule du 120 Ja.
La liste des caractres de 1 z est la
formule de l'lment z.
z.....................................Caractre*
1 H Hydrogne -1s0
2 He Hlium +1s0
3 Li Lithium -2s0
4 Be Bryllium +2s0
5 B Bore -2p-1
6 C Carbone -2p0
7 N Azote -2p1
8 O Oxygne +2p-1
9 F Fluor +2p0
10 Ne Non +2p1
11 Na Sodium -3s0
12 Mg Magnsium +3s0
13 Al Aluminium -3p-1
14 Si Silicium -3p0
15 P Phosphore -3pl
16 S Soufre +3p-1
17 Cl Chlore +3p0
18 A Argon +3p1
19 K Potassium -4s0
20 Ca Calcium +4s0
21 Sc Scandium -3d-2
22 Ti Titane -3d-1
23 V Vanadium -3d0
24 Cr* Chrome
-3d1
25 Mn Manganse -3d2
26 Fe Fer +3d-2
27 Co Cobalt +3d-1
28 Ni Nickel +3d0
29 Cu* Cuivre +3d1
30 Zn Zinc +3d2
31 Ga Gallium -4p-1
32 Ge Germanium -4p0
33 As Arsenic -4p1
34 Se Slnium +4p-1
35 Br Brome +4p0
36 Kr Krypton +4p1
37 Rb Rubidium
-5s0
38 Sr Strontium
+5s0
39 Y Yttrium -4d-2
40 Zr Zirconium
-4d-1
41 Nb* Niobium -4d0
42 Mo* Molybdne -4d1
43 Te Techntium -4d2
44 Ru* Ruthnium +4d-2
45 Rh* Rhodium +4d-1
46 Pd* Palladium +4d0
47 Ag* Argent +4d1
48 Cd Cadmium +4d2
49 In Indium -5p-1
50 Sn tain -5p0
51 Sb Antimoine -5p1
52 Te Tellure +5p-1
53 I Iode +5p0
54 Xe Xnon +5p1
55 Cs Csium -6s0
56 Ba Baryum +6s0
57 La* Lanthane -4f-3
58 Ce* Crium -4f-2
59 Pr Prasodyme -4f-1
60 Nd Nodyme -4f0
61 Pm Promthum -4f1
62 Sm Samarium -4f2
63 Eu Europium -4f3
64 Gd* Gadolinium +4f-3
65 Tb Terbium +4f-2
66 Dy Dysprosium +4f-1
67 Ho Holmium +4f0
68 Er Erbium +4f1
69 Tm Thulium +4f2
70 Yb Ytterbium +4f3
71 Lu Lutcium -5d-2
72 Hf Hafnium -5d-1
73 Ta Tantale -5d0
74 W Tungstne -5d1
75 Re Rhnium -5d2
76 Os Osmium +5d-2
77 lr Iridium +5d-1
78 Pt* Platine +5d0
79 Au* Or +5d1
80 Hg Mercure +5d2
81 Tl Thallium -6p-1
82 Pb Plomb -6p0
83 Bi Bismuth -6p1
84 Po Polonium +6p-1
85 At Astatine +6p0
86 Rn Radon +6p1
87 Fr Francium -7s0
88 Ra Radium +7s0
89 Ac* Actinium -5f-3
90 Th* Thorium -5f-2
91 Pa* Protoactinium -5f-1
92 U* Uranium -5f0
93 Np* Neptunium -5f1
94 Pu Plutonium -5f2
95 Am Amricium -5f3
96
Curium +5f-3
97 Bk Berklium +5f-2
98 Cf Californium +5f-1
99 Es Einsteinium +5f0
100 Fm Fermium +5fl
101 Md Mendlvium +5f2
102 No Noblium +5f3
103 Lr Lawrencium -6d-2
104 Rf Rutherfordium -6d-1
105 Ha Hahnium -6d0
106 Sg Seaborgium -6d1
107 Bh Bohrium -6d2
108 Hs Hassium +6d-2
109 Mt Meitnerium +6d-1
110 Ds Darmstadtium +6d0
111 Uuu Unununium +6d1
112 Cn Copernicium +6d2
113 Lt Lortium -7p-1
114 Fl Flerovium -7p0
115 Gi Gigurium -7p1
116 Lv Livermorium +7p-1
117 Du Dufourium +7p0
118 Qb Qubcium +7p1
119 By Barthlmyum -8s0
120 Ja Janetium +8s0
* C'est le caractre nominal, dterminant la
place de l'lment dans le tableau; il est
gal au nombre d'lectrons dans l'atome.
Le caractre rel de l'lment, voir Annexe 2.
Autres noms:
113 Uut Ununtrium
115 Uup Ununpentium
117 Uus Ununseptium
118 Uuo Ununoctium
119 Uue Ununennium
120 Ubn Unbisnilium
Annexe 2.
Formules des 19 lments irrguliers*.
Je donne z, zt et les lacunes.
Cr 24, 25,(non20)
Cu 29, 30, (non 20)
Nb 41 ,42, (non 38)
Mo 42, 43, (non 38)
Ru 44, 45, (non 38)
Rh 45, 46, (non 38)
Pd 46, 48, (non 37,38)
Ag 47, 48, (non 38)
La 57, 71, (non 57 70)
Ce 58, 71, (non 58 70)
Gd 64 ,71, (non 64 70)
Pt 78,179, (non 56)
Au 79,80, (non 56)
Ac 89,103, (non 89 102)
Th 90,104, (non 89 103)
Pa 91,103, (non 91 102)
U 92, 103, (non 92 102)
Np 93,103, (non 93 102)
Cm 96, 103, (non 96 102)
Prsomption. Je prsume que les lments
z suprieur 96 sont tous rguliers.
Annexe 3.
Les 120 lments, leurs blocs par effets Zeeman et
Pauli sous la forme d'querres.
Effet Pauli, spin-, spin+. Effet Zeeman 1, 3, 5, 7.
. .
.
Fig. A1. Dans le tableau, l'ordre est ainsi:
valeurs spin - de l'lectron d'abord, puis spin +, ce qui tablit une moiti
Ouest et une moiti Est. C'est l'effet Pauli. Ensuite l'effet Zeeman,
gnrateur d'querres qui s'embotent. Rf. 1.
Une querre ayant des bras non nuls pointe
ncessairement vers l'une de 4 orientations intermdiaires entre les points
cardinaux. Une querre ayant des bras nuls pointe vers ces 4 orientations.
Voici la collection des querres logeant une fois
chacun des 120 lments. Figs A2, A3.
.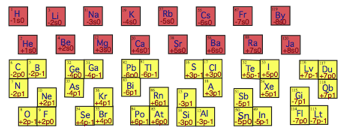 .
.
Fig. A2. Les 16 querres s sans bras. Je les nomme
par le seul lment qu'elles contiennent: 1 H, 2 He, 3 Li, 4 Be, 11 Na, 12 Mg,
19 K, 20 Ca, 37 Rb, 38 Sr, 55 Cs, 56 Ba, 87 Fr, 88 Ra, 119 By, 120 Ja.
Les 12 querres ayant ayant 2 bras d'une
case. Je les nomme par le 1er des lments qu'elles contiennent, dans l'ordre:
5 B, 8 O, 13 Al, 16 S, 31 Ga, 34 Se, 49 In, 52 Te, 81 Tl, 84 Po, 113 Uut ou Lt,
116 Lv, Parmi ces querres, 3 sont orientes NO, 3 orientes SE, 3 orientes SO
et 3 orientes NE.
image017.pct, HHeLtFl.ai
. .
.
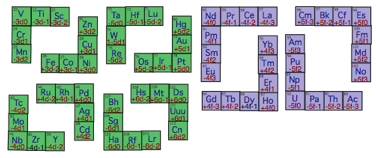
Fig. A3. Les 8 querres d ayant 2 bras de 2
cases. Je les dsigne par le 1er des lments qu'elles contiennent: 21 Sc, 26
Fe, 39 Y, 44 Ru, 71 Lu, 76 Os, 103 Lr, 108 Hs.
Parmi ces querres, 2 sont orientes NO, 2
orientes SE, 2 orientes NE et 2 orientes SE.
Les 4 querres f ayant 2 bras de 3 cases. Je
les dsigne par le 1er des lments qu'elles contiennent: 57 La, 64 Gd, 89 Ac,
96 Cm
Parmi ces querres, une est oriente NO,
une oriente NE, une oriente SO et une oriente SE,
image019.png, VTiThAc.ai,
Rgle
7. Sens de rotation. Il me
faut choisir un sens de rotation dans les querres ayant des bras non nuls. Je
cre la 1re querre ainsi rencontre BCN dans le sens de rotation anti-horloge.
Cela est dterminant pour la cration des autres querres prsentes Figs 8, 9
et l'occupation des cases des carrs des strates 2, 3 et 4
Sens de rotation. Rotation anti-horloge dans
les quadrants NO e SE, rotation horloge dans les quadrants SO et NE. La rgle
s'nonce ainsi:
Rotations dans les quadrants: NO et SE: rotation
anti-horloge; SO et NE: rotation horloge. Les flches incurves Fig. 10.
.. 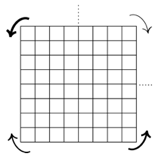
Fig. A3.
L'criture est anti-horloge aux quadrants NO et SE, horloge aux
quadrants SO et NE. flches.png
L'ordre du remplissage des quadrants est
selon l'paisseur des traits des flches.
Muni de ces querres, je m'affaire meubler
les strates 1, 2, 3, 4. Ici je remarque que la 1re querre B, C, N rencontre,
place au plus prs du centre de figure dans le quadrant NO, dsigne un carr
ayant 4 cases de ct. Je place immdiatement en regard la 2e querre 8 O. Fig.
11.
Voici les tapes du remplissage de la strate
1 par les 4 querres sans bras. Fig. A4.
. ![]() .Source H utilise, valeurs n et l: 1 0, 2 0.
.Source H utilise, valeurs n et l: 1 0, 2 0.
Fig. A4. En 4 tapes, le remplissage de la
strate 1 en 4 tapes par les 4 querres sans bras de 1 H 4 Be. Les
strates1et221h157XII2014, 2.Publication
Voici les 8 tapes du remplissage de la
strate 2 par 8 querres. Fig. A5.
.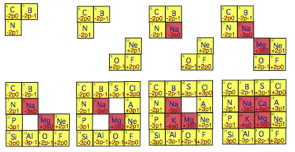 . Source H utilise, valeurs n et l: 2 1, 3 0; 3 1, 4 0.
. Source H utilise, valeurs n et l: 2 1, 3 0; 3 1, 4 0.
Fig. A5. En 8 tapes, le remplissage de la
strate 2 en 8 tapes par 8 querres de 5 B 20 Ca. Les
strates1et221h157XII2014.
Voici les tapes du remplissage de la strate
3 par 12 querres. Fig. A6.
.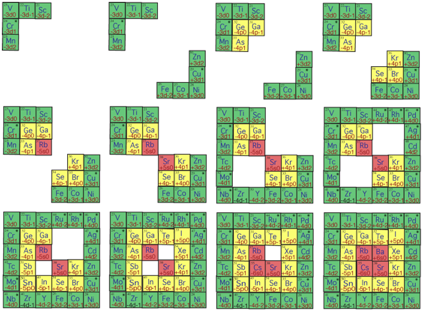 . Source H utilise,
valeurs n et l: 3 2, 4 1, 5 0; 4 2, 5 1, 6 0.
. Source H utilise,
valeurs n et l: 3 2, 4 1, 5 0; 4 2, 5 1, 6 0.
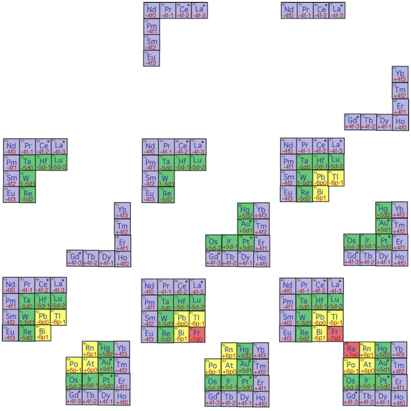
Fig. 13. Les 12 tapes du remplissage de la
3e strate, de 21 Sc 56 Sr, par 12 querres s, p et d.
ScBa9hyclesirrguliers5010XII2014, 2.Publication
.  .
.
Fig. 14. Strate 4. Les 8 premires tapes sur
16 du remplissage de la strate 4, de 57 La 88 Ra, par les querres s, p, d et f. LaRaycirrguliers18h4710XII2014.png,
2.Publication
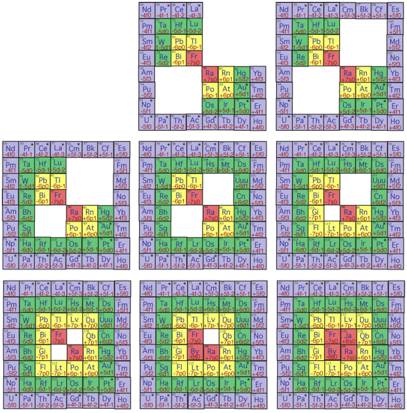 . Source H utilise, valeurs n et l: 4 3, 5 2, 6 1, 7 0; 5 3, 6 2, 7 1, 8
0.
. Source H utilise, valeurs n et l: 4 3, 5 2, 6 1, 7 0; 5 3, 6 2, 7 1, 8
0.
Fig. 15. Strate 4. Suite et fin du
remplissage de la strate 4, les 8 dernires tapes. 89 Ac 120 Ja.
AcJaycirrguliers18h2010XII2014.png, 2.Publication
Et voici la totalit des remplissages
accomplis, sous la forme d'un tableau des lments en demi-ellipse. Fig. 16.
.
.  .
.
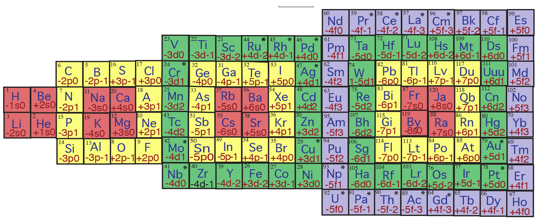
Fig. 16. D'aprs ci-dessus, tableau des
lments en demi-ellipse. H Ja y compris irrguliers11XII2014.png,
2.Publication LaDemiEllipse2015-02-12 à 17.34.58.png
Ainsi se trouve obtenu, par 7 rgles
gomtriques, le tableau en demi - ellipse, qui manifeste une symtrie 4 et
rpond au nombre magique 30.
Annexe 4. Affichage pseudo-bidimensionnel.
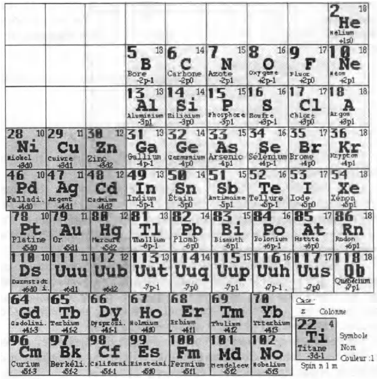
Voici le Tableau de Mendeleev, tel que je l'ai prsent papier et en ligne ds 2004, contenant 118 lments. Rf. 11.
.17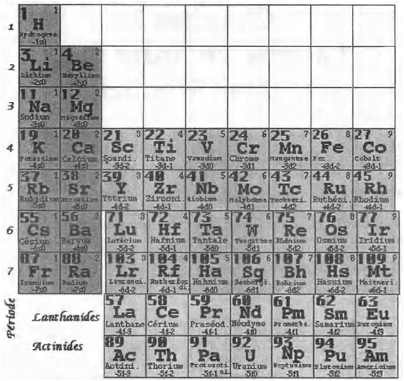 .
. .18.
.18.
Figs 17, 18. Tableau de Mendeleev, forme brve, 118 lments, de 1 H 118 Qb; HàAm2015-05-04.png, HeàTi2015-05-04.png
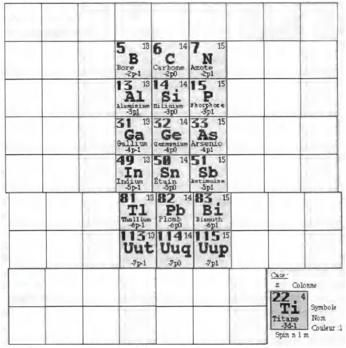
Voici le tableau de Mendeleev de forme brve en ne gardant que les 59 lments de spin -. Figs 19, 20.
.19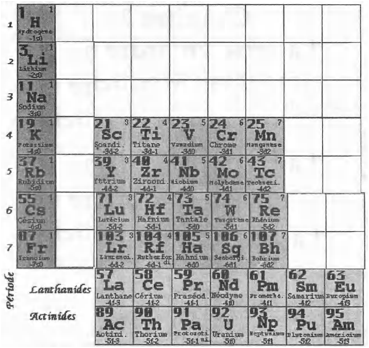 .
. .20
.20
Figs 19, 20. Tableau
de Mendeleev, forme brve, les 59 lments de spin -, de 1 H 115 Uup; HàAm2015-05-04m.png,
HeàTi2015-05-04m.png
Et voici le tableau de Mendeleev de forme
brve en ne gardant que les 59 lments de spin +. Figs 21, 22.
.21 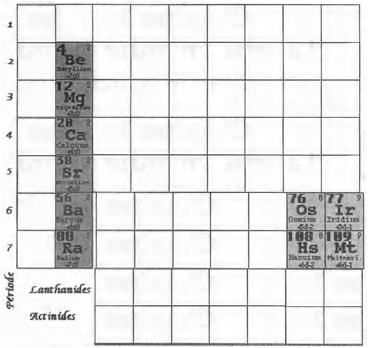 .
. 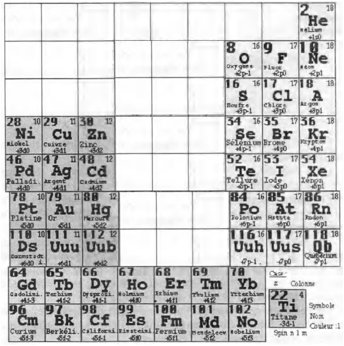 22
22
Figs 21, 22. Tableau de
Mendeleev, forme brve, les 59 lments de spin +, de 1 He 118 Qb; HàAm2015-05-04p.png,
HeàTi2015-05-04p.png
Remerciements.
Ë mon fils Thierry Leroux-Demers, merci pour des discussions
profitables.
Rfrences.
Rf. 1. Pierre Demers 2015, http://lisulf.quebec/HetJa.htm
Rf. 2. Patrick Callet 2004, 2015 . http://lisulf.quebec/Quebecium_Callet_1_4min46.mpg
Problmes techniques.
Rf. 3. Patrick Callet 2015, 2015
Quebecium Callet 2_compressé35min53.avi http://lisulf.quebec/Quebecium_Callet_2_35min53.avi
Problmes techniques.
Rf. 4. Systme du Qubcium. ![]() Pierre Demers 2015. Systme du Qubcium. Tableau 3D en boules de
H Ja, 4I2015, Version du 21I2015. Traduction interdite.
Pierre Demers 2015. Systme du Qubcium. Tableau 3D en boules de
H Ja, 4I2015, Version du 21I2015. Traduction interdite.
http://lisulf.quebec/Tableauenboules3DboulesHJa.htm
Rf. 5. Sur la synthse de
l'lment 118. 2009
http://www.webelements.com/ununoctium/
http://fr.wikipedia.org/wiki/Ununoctium,
http://www.webelements.com/ununoctium/
Ces articles restent muets au sujet du Systme du Qubcium.
Rf. 6. ![]() Pierre Demers 2013.
Communiqu de presse 2007. Systme du Qubcium. Systme
du Qubcium. Trente. Communiqu de presse.
Pierre Demers 2013.
Communiqu de presse 2007. Systme du Qubcium. Systme
du Qubcium. Trente. Communiqu de presse.
Rf. 7. recteur.umontreal.ca/index.php?id=1421&tx_ttnews[tt_news]=2330&tx_ttnews[backPid]=1547&no_cache=1
"...les rseaux
internationaux de la recherche en astronomie et en arospatiale et contribue
repousser toujours plus loin nos connaissances sur lÕUnivers ...
"...pour toute
personne qui sÕintresse la science au Canada."
(Une pense pour le
Qubec?)
Rf. 8. http://www.ledevoir.com/politique/canada/431555/l-observatoire-du-mont-megantic-survivra
LÕObservatoire du
Mont-Mgantic survivra pour au moins deux ans 11 fvrier 2015 20h52 |Mlanie Marquis - La
Presse canadienne | Canada
PiD. Mieux que rien?
Quelle piti que la science du Qubec soit une fois de plus la merci d'un
gouvernement qui ne veut pas de nous depuis 1982 et qui prend l'argent dans nos
poches pour le distribuer et perptuer son autorit illgitime. -
Mangerons-nous encore longtemps le pain de la captivit?
Le
dput libral de Westmount–Ville-Marie au fdral, Marc Garneau, a
dnonc lÕidologie du gouvernement Harper en ce qui concerne le financement de
la recherche au Canada. Ç Ce
gouvernement a clairement donn le message, il y a quelques annes, quÕil
dsirait favoriser la recherche applique qui aboutit des dbouchs
commerciaux, plutt que la recherche fondamentale, comme lÕastronomie qui
accrot notre connaissance de lÕUnivers È,
Le Systme du Qubcium, lui
aussi, augmente nos connaissances sur l'Univers.
Rf. 9. Patrick Callet 2007-2015. Reconstirution virtuelle de l'Abbaye
de Royaumont.
http://www.royaumont.com/fr/actualite/reconstitution-virtuelle-de-l-abbatiale
Reconstitution virtuelle de l'abbatiale. En 1792 sÕcroulait, sous la
traction de centaines de bÏufs, celle qui tait considre comme lÕune des plus
belles glises de lÕordre de Cteaux : dcouvrez aujourdÕhui la reconstruction
numrique en trois dimensions de lÕglise dans son tat mdival.Fin 2010, la
Fondation Royaumont a t sollicite par Patrick Callet, chercheur lÕcole
Centrale de Paris, qui proposait de donner comme projet dÕtudes des
tudiants de 2e anne la ralisation dÕune maquette numrique de lÕglise
abbatiale de Royaumont, dtruite en 1792.
Rf. 10. Pourquoi?
Le 2015-04-06 13:01, Thierry Leroux-Demers
<lerouxdemers@gmail.com> a crit :
Bon point. Merci.
Envoy de mon iPhone
Le 2015-04-06 09:51, Demers Pierre
<pierre.demers@lisulf.quebec> a crit :
Pourquoi arrter z = 120 ni avant ni aprs?
Parce quÕainsi on se trouve assurer la 2e
moiti de la 4e strate une organisation semblable celle de la 1re moiti,
comme cÕest le cas pour les strates prcdentes, la 1re, la 2e et la 3e;
chaque moiti de strate est une priode.
En dÕautres paroles, la 8e devient semblable la 7e,
laquelle est entirement connue, du La 57 au Ra 88. Elle sÕtend du Fr 87 connu
au Ja 120 spculatif.
Ensemble hier jour de Pques 2015.
Saluts XXX.
GPPi lundi de Pques 2015 il est 9h50
Rf. 11. Systme du Qubcium. 2004 ![]() Pierre Demers. La nouvelle Classification
des lments. PUM. ISBN 2-9802454-7-X
Pierre Demers. La nouvelle Classification
des lments. PUM. ISBN 2-9802454-7-X
En 2015 PUM Presses Universitaires de Montral est
devenue PPD Presses Pierre Demers.