QbSyst2e.24.html
Système du Québécium
Suivant QbSyst2e.25.html
Précédents QbSyst2e.23quater.html QbSyst2e.23bis.html
Chapitre 17
Application à la classification des éléments
Tableaux 3D

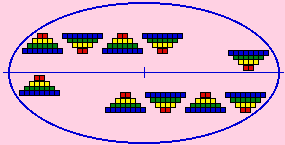
Fig. 303.
Pyramides à base carrée. Pyramide du québécium.
Une forme tridimensionnelle fort simple du Tableau No 3 (figure 278) se présente immédiatement : on remplace les cases planes par des cubes que nous pouvons appeler cases cubiques et on empile les strates, la plus petite au sommet ou plutôt à la base ce qui simplifie la sustentation du montage. Le résultat est une pyramide à base carrée. Par généralisation, nous l'appellerons un tableau tridimensionnel.
La pyramide devient un jeu de cubes pour enfants, mais peut-être trop considérable avec ses 120 cubes. En la réduisant aux 20 cubes nécessaires pour constuire les strates 1 et 2, ce serait un autre jeu de cubes pour leur apprendre 20 des éléments chimiques en plus des 26 lettres de l'alphabet et les 10 chiffres. Plus tard, ils auraient la révélation qu'il existe 100 autres éléments et leur apprentissage répèterait le cours de l'histoire.
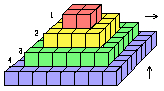
Fig. 304. Pyramide 3D résultant de la superposition des strates 1, 2, 3, 4. Les strates peuvent s'isoler par un glissement horizontal et les cheminées peuvent s'isoler par un déboîtement vertical.
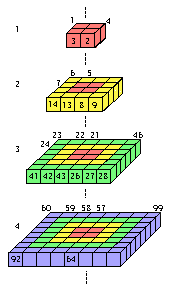
Fig. 305. Pyramide des éléments éclatée. Les 4 strates ont été séparées par glissement et alignées. Plus ou moins rapprochées verticalement, elles forment le Tableau No 7 (3D). Affectations des cases : on donne les valeurs de Z de quelques cases seulement. Le plan complet des valeurs de Z se lit à la figure 278.
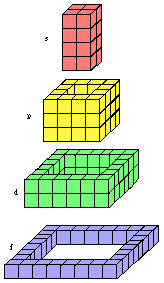
Fig. 306. Les 4 cheminées s, p, d, f isolées par déboîtement vertical.
Deux fractionnements sont évidents, effectués par mouvements orthogonaux : en cheminées verticales par déboîtement vertical et en strates horizontales par glissement vertical et alignement. Figures 305, 306.

Fig. 307. Les cheminées s, p, d, f rendues visibles au complet étant portées par une infrastructure. Au total 200 cubes.
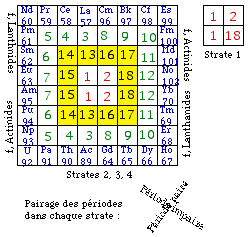
Fig. 308. IUPAC. Plan d'occupation des cheminées du tétraèdre du québécium par les 18 groupes numérotés de l'IUPAC, avec addition des lanthanides et des actinides. Plan distinct pour la strate 1.
La continuïté des groupes apparaît sans difficulté, elle est verticale. Les groupes forment des empilements dans ce que nous appellons des cheminées qui s'emboîtent et se déboîtent. Figures 304, 305.
Les cheminées peuvent se définir comme une collection d'empilements de symétrie verticale 4. Elle sont des empilements de couronnes. La cheminée centrale se résume à une tour quadrangulaire sans ouverture pour la fumée. La cheminée extérieure ressemble à une clôture basse d'une couronne seulement. - On peut encore appeler cheminée un empilement ayant une seule case cubique à chaque niveau.
Le plan des cheminées ressemble à l'organisation de la strate 4. Ce plan comporte les 18 groupes officialisé par l'IUPAC, qui sont ici associés à des empilements et en outre les lanthanides et les actinides. Le plan de la strate 1 en termes des groupes de l'IUPAC est distinct du plan des strates 2, 3, 4 qui suivent à cause de He que l'IUPAC classe dans le groupe 18.
En strates : on rencontre les périodes pairées horizontalement de 1 à 8; par cheminées : on rencontre les couronnes qui isolent les blocs s, p, d, f et les valeurs du quantum azimutal l = 0, 1, 2, 3. Ce qui est d'intérêt pédagogique et en même une satisfaction pour l'esprit.
En cheminées, les 18 groupes de l'IUPAC se retrouvent en doublé, avec en plus l'annexe des blocs f, lanthanides et actinides dans la cheminée f. Chaque groupe de l'IUPAC est présent sous la forme de 2 empilements d'un cube, parties d'une cheminée, ces deux empilements étant de symétrie par rapport à l'axe vertical. La strate 1 fait exception : elle a une case 18 au lieu de 2.
Les cubes de la pyramide ne sont pas tous visibles de l'extérieur. Pour remédier à cet inconvénient, on peut isoles les cheminées (figure 305), ou encore les soulever et les installer sur une infrastructure nécessitant 80 cubes (figure 307). Des vues en plan pour chacune des 4 strates permettent de repérer les valeurs de n et de l et l'affectation de chaque cube, ces vues existent à la figure 278.
La figure 305 montre un aperçu de l'affectation des cases cubiques dans les strates de la pyramide.
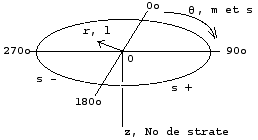
Fig . 309. Coordonnées cylindriques r,
q, z dans la pyramide du québécium et nombres quantiques.Orbitales. Les cases de symétrie 2 par rapport à l'axe vertical dans une cheminée sont partenaires d'une même orbitale. Cela est vrai pour toutes les strates.
Tétrades. Les cases de symétrie 4 par rapport à l'axe vertical dans une cheminée sont partenaires d'une tétrade.
Coordonnées cylindriques.
Les cases de la pyramide se prêtent à une description 3D en coordonnées cylindriques r,
q, z qui ne peuvent prendre que des valeurs quantifiées correspondant aux centres de chaque case cubique. Les correspondances avec les nombres quantiques d'un état électronique n, l, m, s ne sont pas toutes uni-univoques. Le No de la strate apparaît et il correspond à 2 numéros de période, mais ces numéros ne sont pas parmi les nombres quantiques n, l, m, s. Tableau 71, figure 309.La distance de l'axe r s'évaluera de préférence en termes de numéros de la couronne, allant de 0 à 3; on pourrait donc parler de coordonnées quadrangulaires Il n'y a pas de correspondance uni-univoque entre l'une quelconque de ces coordonnées et la valeur du quantum principal n ou le numéro de la période. La seule correspondance uni-univoque entre ces coordonnées et l'un des nombres quantiques est entre r et l : l augmente de façon discontinue de 0 à 3 avec l'augmentation de r.
s dépend de
q seulement mais q dépend de m et s, soit une correspondance bi-univoque. 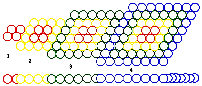
Fig. 310. La grille des 120 cases sphériques formée en 4 losanges. Vue en plan, vue de côté.
Tableau 71. Coordonnées cylindriques et nombres quantiques dans la pyramide du québécium .
z : No de la strate, fonction du numéro de la période, fonction de n et l;
r : quantum azimutal l;
q
: quantum magnétique m et spin s.On voit que la classification 3D dans la pyramide du québécium attribue un rôle secondaire à n. Il en va de même pour la classification 2D dans la grille du québécium plane.
Cases sphériques en 2D, en 3D, replis.
Remplaçons les cases de la grille 2D par des sphères. Leur assemblage, dans chaque strate, se prête à des déformations conduisant à des arrangements compacts en losanges décrits au Chapitre 1, figures 18 ssq. Les 120 cases prennent l'aspect de la figure 310.
La déformation imposée introduit une dissymétrie qui peut se décrire partiellement comme un cisaillement de 30o vers la droite. Les symétries entre cases, qui étaient associées à des droits, sont changées.
![]()
Fig. 311. Chaque strate donne par repli un tronc de tétraèdre, dont on montre ici une face.
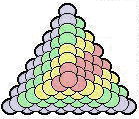
Fig. 312. Tétraèdre du québécium. Vue en plan. Deux faces sont d'aspect semblable.
L'intérêt principal de cette grille en losange est qu'elle se prête au repli expliqué figure 20, une strate à la fois. Chaque strate donne un empilement en forme de tronc de tétraèdre régulier évasé vers le bas. La strate 1 donne un empilement en forme de tétraèdre. Figure 311.
Ces troncs de tétraèdre peuvent s'assembler pour donner un tétraèdre du québécium ou tétraèdre des éléments. Figure 312.
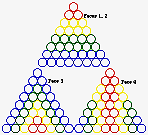
Fig. 313. Tétraèdre du québécium, vue des 4 faces.
L'assemblage de ces troncs conduit à un tétraèdre régulier ayant 8 boules de côté, comme à la figure 23, où chaque strate occupe 2 niveaux. La figure 312 en montre le plan. et la figure 313 en montre les 4 faces, 2 d'entre elles ayant même aspect.
Voici comment les éléments s'y présentent, niveau par niveau. Figure 314.
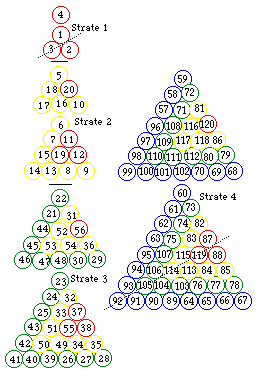
Fig. 314. Tétraèdre du québécium obtenu par repli. 4 strates ayant chacune 2 niveaux. Valeurs de Z.

Fig. 315. Encastrement de 4 boules pour donner des tétraèdres (des tétrades). - de 4 tétrades pour donner un tronc tétraédrique. Vues en plan, vue de côté.
Symétries 4, orbitales et tétrades (tétrades jointives).
La figure 314 possède les symétries du tétraèdre régulier; elle est de symétrie 4 dans l'espace si on considère toutes les boules comme égales. Par les centres des boules, on dessine un tétraèdre régulier. Quant à l'occupation par les boules de même valeur de l, elle est de symétrie 2; à cet égard, la figure admet un plan de symétrie binaire défini par les centres des boules 4, 92 et 120, tel que figuré par un pointillé à la figure 314.
Les éléments forment 60 orbitales et 30 tétrades. Voyons si nous pouvons repérer ces structures. Il serait intéressant de les rendre manifestes et réunies dans le tétraèdre.
Lorsque nous parlons précisément d'une structure en tétrades, il s'agit bien sûr de tétrades jointives, puisque les tétrades sont touours présentes mais pas toujours jointives.
Tableau 72. Les tétrades.
Strate 1
s1 : 1, 2, 3, 4.
Strate 2
s11 : 11, 12, 19, 20.
p5: 5, 8, 13, 16;
p6: 6, 9, 14, 17;
p7: 7, 10, 15, 18.
Strate 3
s37: 37, 38, 55, 56;
p31: 31, 34, 49, 52;
p32: 32, 35, 50, 53;
p33: 33, 36, 51, 54.
d21: 21, 26, 39, 44;
d22: 22, 27, 40, 45;
d23: 23, 28, 41, 46;
d24: 24, 29, 42, 47;
d25: 25, 30, 43, 48.
Strate 4
s87: 87, 88, 119, 120;
p81: 81, 84, 113, 116;
p82: 82, 85, 114, 117;
p83: 83, 86, 115, 118;
d71: 71, 76, 103, 108;
d72: 72, 77, 104, 109;
d73, 73, 78, 105, 110;
d74: 74, 79, 106, 111;
d75: 75, 80, 107, 112.
f57: 57, 64, 89, 96;
f58: 58, 65, 90, 97;
f59: 59, 66, 91, 98;
f60: 60, 67, 92, 99;
f61:61, 68, 93, 100;
f62: 62, 69, 94, 101;
f63: 63, 70, 95, 102.
Tel que le tétraèdre se présente figure 314, on y repère les 4 tétrades s sous forme jointive : s1, s11, s37 et s87. Ce sont les seules tétrades jointives qu'il contient. Le processus de repli, tel qu'appliqué, est un mauvais fournisseur de tétrades jointives. On peut en dire autant, d'ailleurs, du processus de confection des tableaux d'éléments 2D pratiqués jusqu'ici.
Il serait intéressant de réaliser une répartition des boules de la figure 314 qui ferait l'union de chacune des tétrades, qui réaliserait des tétrades jointives, et nous allons voir qu'en définitive, chaque strate individuellement et le tétraèdre du québécium tout entier se prêtent effectivement à une structuration complète en tétrades. Il y a là quelque chose qui évoque un pavage, mais imparfaitement, puisqu'il y a des interstices entre les boules.
Encastrement.
Cet analogue d'un pavage mérite le nom d'encastrement. Quatre boules s'encastrent pour donner un assemblage compact où chaque boule en touche 3, dessinant un tétraèdre régulier par leurs centres. Quatre tétrades s'assemblent par encastrement pour dessiner un tronc de tétraèdre d'arête double du précédent. Figure 315.
Nous allons examiner le problème de la structuration de chaque strate à tour de rôle et en déduire des principes de classification qui s'imposent impérativement pour des raisons de symétrie.
Strate 1.
La strate 1 est une tétrade s1 à elle seule : H1, He2, Li3, Be4 qui est nécessairement jointive.
Strate 2.
Voyez la figure 314.
Voyez les tétrades s et p au Tableau 73. Seule la tétrade s est réunie.
Pour former une tétrade jointive entre boules à l'intérieur d'une strate, il faut 3 boules jointives dans un niveau et une boule isolée en regard dans l'autre niveau, ou bien 2 boules dans chacun des niveaux. Nous laissons de côté cette 2e possibilité. Les schémas de tétrades jointives qui nous intéressent sont de 4 types : dessinant un A ou un V, 3 boules en bas ou n haut. Tableau 74 et figure 318.
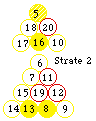
Fig. 316. Strate 2 d'après la figure 314. La tétrade s est réunie, les tétrades p ne le sont pas.
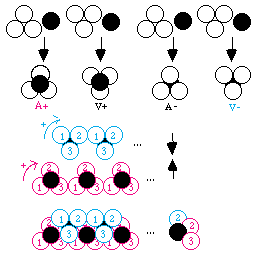
Fig. 317. Quatre types de tétrades jointives sur deux niveaux. En A ou en V; 3 boules en bas, 1 en haut; 3 en haut, 1 en bas. Les types A+ et V- se prêtent à des assemblages jointifs par encastrement. Il apparaît des espèces de barres dont on montre une vue latérale. Notez la numérotation des boules, dans le sens droit en commençant à gauche sur la ligne de 2 boules.
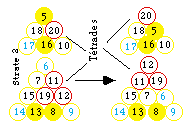
Fig. 318. Strate 2. Transposition , à l'intérieur de la strate , de la tétrade s la portant en sommet de figure.
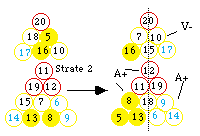
Fig. 319. Strate 2 en 4 tétrades jointives. En pointillé, plan de symétrie binaire touchant les tétrades de l'épine dorsale.
Tableau 74. Types de tétrades.
Dessine un A
.....3 boules en bas, 1 boule en haut.....A+Dessine un A
.....3 boules en haut, 1 boule en bas.....A-Dessine un V
.....3 boules en bas, 1 boule en haut.....V+Dessine un V
.....3 boules en bas, 1 boule en haut.....V-Deux types nous suffiront : A+ et V-.
Si nous voulons que les tétrades p soient réunies dans la strate 2, nous ne pouvons pas laisser la tétrade s où elle est. En effet, il faudrait disposer de 3 groupes de 3 boules jointives p appropriées dans un même niveau.
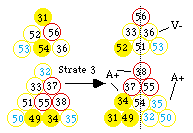
Fig. 320. Strate 3, cases s et p, remaniées afin de donner 4 tétrades jointives. En pointillé, plan de symétrie binaire touchant les tétrades de l'épine dorsale.
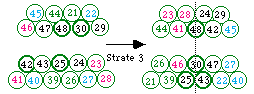
Fig. 321. Strate 3, cases d organisées en tétrades.
Or une telle disponibilité n'existe pas. Il nous faut réaliser une transposition des boules en jouant à l'intérieur des deux niveaux de la strate. La transposition choisie place la tétrade s à un sommet du tronc tétraédrique. La tétrade s est du type A+. La transposition apparaît figure 318.
Il faut ensuite réarranger les 12 boules p. Une possibilité est celle de la figure 318. La colonne vertébrale se manifeste sous la forme de 2 tétrades axiales, traversées par un plan de symétrie binaire de la strate 2 et renfermant les gaz rares. Les tétrades sont de 2 types exclusivement A+ et V-. Trois tétrades A+ occupent les sommets du triangle tracé par la strate 2, une tétrade V- occupe le centre de ce triangle.
La tétrade p7 appartient à la colonne vertébrale.
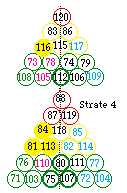
Fig. 322. Strate 4, cases s, p, d organisées en tétrades.
L'ordre numérique des tétrades p commence à gauche et procède en va-et-vient pour aboutir au centre:
p5, p7, p6.
Strate 3.
Cases s et p. Occuponns-nous d'abord des cases s et p. Tableau 73.
Les cases s et p (figure 314) occupent un triangle aussi bien dans cette strate que dans la strate 2, ce qui suggère de procéder sde la même manière que pour la strate 2, avec simple changement de numéros. Le résultat est à la figure 320.
De plus, il paraît tout indiqué de déplacer ce triangle par translation pour qu'il occupe le sommet de la figure. Les cases d viennent toutes à la base.
Cases d. Voyez les tétrades au Tableau 73.
La tétrade d25 sera placée au centre afin qu'elle participe à l'épine dorsale. Les numéros commenceront à gauche, donc d21 est à gauche et ce doit être une tétrade du type A+ puisqu'elle est à un sommet du triangle. Les 5 types successifs sont ainsi :
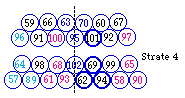
Fig. 323. Strate 4, cases f organisées en tétrades.
A+, V-, A+, V-, A+.
d25 est centrale et donc l'ordre numérique doit être en va-et-vient :
d21, d23, d25, d24, d22.
Cela est fait à la figure 321.
Strate 4.
Cases s, p, d. L'exemple de la strate 3 s'applique,avec changements de numéros, aux présentes cases s, p, d.Voyez les tétrades au Tableau 73. La figure 322 montre le résultat.
Cases f. Voyez les tétrades f au Tableau 72. La figure 323 montre le résultat.
Le tétraèdre du québécium en tétrades.
Il nous reste à assembler les strates et les morceaux de strates des figures 318 à 322 afin de réaliser le tétraèdre des éléments et des électrons du québécium en tétrades (jointives).
On donne ainsi le tétraèdre du québécium structuré en tétrades, figure 323, et ce même tétraèdre en tableau détaillé, tableau No 8 3D à la figure 324. Dans ces figures, on 'est efforcé de rendre visibles les tétrades A+ de 3 boules surmontées d'une et les tétrades V- d'une boule surmontée de 3. Dans une tétrade, on peut reconnaître les éléments partenaires de 2 orbitales homologues l'une de l'autre dans des périodes voisines.
Fig. 324. Tétraèdre du québécium structuré en tétrades. Chaque strate est en deux niveaux. Le centre des niveaux est marqué. Valeurs de Z.
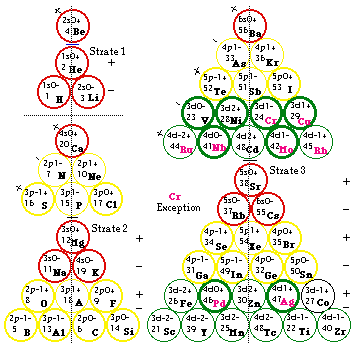
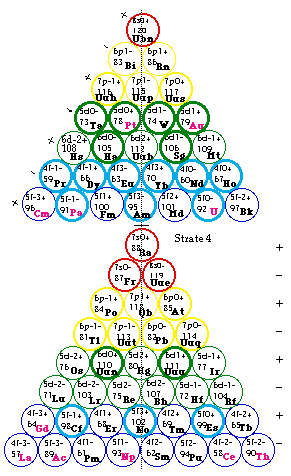
Fig. 325. Tétraèdre du québécium structuré en tétrades. Tableau détaillé 3D. Tableau No 8. Tétrades en A+ (15) et en V- (15).
La présente structuration établit un plan de symétrie qui traverse les tétrades de l'épine dorsale. Les étapes de stabilité dans la genèse du tableau des éléments comprennent plus que les gaz rares, seuls considérés par la plupart des auteurs dans l'établissement des récurrences : elles comprennent en outre les autres éléments de l'épine dorsale. Le présent tétraèdre les met en évidence. (Figure 326).
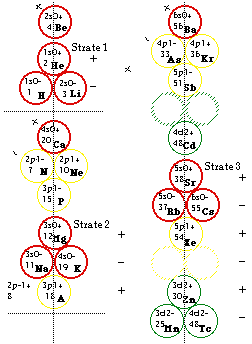
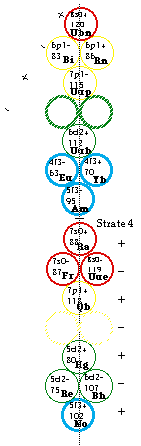
Fig. 326. Épine dorsale dans le tétraèdre du québécium.
Pour cause de construction, les spins + et - alternent régulièrement par rangées horizontales aux niveaux inférieurs des strates et par rangées obliques aux niveaux supérieurs des strates. Les exceptions sont figurées : noter comme elles s'accumulent loin du sommet des figures en évitant la colonne vertébrale, laquelle est figurée séparément à la figure 326.

Fig. 327. Tétraèdre des éléments, nouvelle version. Vue en plan. Les faces sont d'aspect semblable 2 à 2.
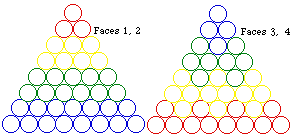
Fig. 328. Tétraèdre des éléments, nouvelle version. Vue des 4 faces.
Symétries.
Le tétraèdre du québécium.dans sa nouvelle version que nous venons de décrire a gagné en symétrie. Vaudrait-il mieux l'appeler tétraèdre des éléments puisque la même forme géométrique peur s'appliquer aux biomolécules? Peut-être, sauf que l'appellation québécium rappelle qu'il s'agit autant de l'élément 118 que de tous les autres qu'il contient.
Si on considère l'occupation par les boules de même valeur de l, les faces présentent maintenant deux aspects seulement, au lieu de trois dans la version obtenue immédiatement par repli. Comparez les figures 312 et 313 avec les figures 327 et 328.
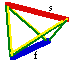
Fig. 329. Le tétraèdre des éléments schématisé par 2 barres orthogonales et 4 ficelles. Barre des éléments s en haut, barre des éléments f en bas. Les ficelles sont les éléments p et d.
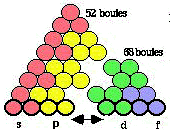
Fig. 330. Assemblage et désassemblage du tétraèdre des éléments en deux blocs : éléments réguliers s et p et de transition d et f. Vue latérale.
La nouvelle version conduit à une représentation schématique remarquable : deux de ses arêtes opposées sont entièrement composées de valeurs uniques de l. Pour l'une d'elles, l=0, pour l'autre, l=3. En couleurs symboliques, l'une est rouge et l'autre est bleue. De plus, elles sont orthogonales sans se rencontrer. Cette orthogonalité géométrique s'accorde avec le contraste des propriétés des éléments s et f, les uns de valence unité ou double et principalement stables, les autres de valences multiples et peu stables électroniquement. L'instabiité électronique des éléments f va d'ailleurs de pair avec leur instabilité nucléaire, ces instabilités étant liées dans les deux cas à la complexité des structures.
Cette schématisation géométrique peut s'accentuer encore : le tétraèdre des éléments peut s'évoquer dans l'espace par deux baguettes égales, l'une rouge et l'autre bleue, munies de quatre ficelles joignant leurs extrémités deux à deux. Les ficelles sont colorées en jaune et en vert. On tient l'une des baguettes horizontalement, l'autre se place d'elle-même. On pourrait autant parler d'une stylisation. Figure 329.
Cette simplification à l'extrême du tableau des éléments fait contraste avec les premières représentations obtenues par les pionniers des siècles passés. Elle était inconcevable en l'absence des éléments f.
L'assemblage se prête à une décomposition par désencastrement en éléments réguliers s et p d'un bord et éléments de transition d et f de l'autre bord. Figure 330.

Fig. 331. Agencement des boules au voisinage du centre des niveaux dans le tétraèdre structuré en tétrades. Réf. figure 324.
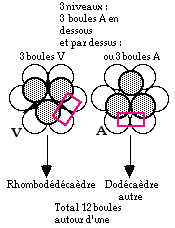
Fig. 332. Formation du rhombododécaèdre pavant et du dodécaèdre autre. Assemblage en A ou en V. 12 points de contact de la boule centrale. Certaines boules dessinent des carrés.
Tétrades en boules, tétrades en solides pavants.
Dans la figure 324. prenons l'exemple de la boule 18. Elle touche 6 boules au même niveau, 3 autres disposées en V par dessus et 3 autres disposées en A en dessous, soit 12 points de contact. Par chacun de ces points passe un plan tangent. Ces 12 plans se rencontrent et délimitent un dodécaèdre aux faces losanges ou rhombododécaèdre. Il a 6 sommets 4, et 8 sommets 3 résultant de la rencontre de 4 et de 3 plans respectivement. Figures 331, 332.
Chaque boule des tétrades et du tétraèdre peut être remplacée par un tel rhombododécaèdre et leur assemblage est jointif. Nous avons donc trouvé un moyen de paver le tétraèdre des éléments en tétrades de rhombododécaèdres.
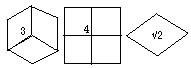
Fig. 333. Le rhombododécaèdre. Sommet 3, sommet 4, une face losange. Les diagonales du losange sont entre elles comme 1 et Ã2.
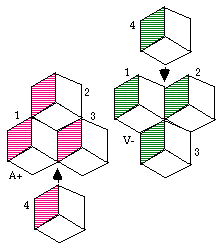
Fig. 334. Tétrade de type A+ : 4 vient par dessus 1, 2, 3.; de type V- : 4 vient en dessous de 1, 2, 3.
Il faut savoir que 3 niveaux successifs de boules peuvent être organisés de deux manières. Dans les deux cas, une boule centrale en touche 12, mais les boules des niveaux en dessous et par dessus peuvent être les unes disposées en A et les autres en V ou toutes selon la même lettre. Dans ce dernier cas, les faces du dodécaèdre ne sont pas toutes des losanges; 6 d'entre elles sont des trapèzes. Figure 332.
Voici l'aspect d'un rhombododécaèdre. Figure 333.
Voici comment les rhombododécaèdres s'assemblent 4 à la fois pour donner des tétrades A+ et V-. Le rhombododécaèdre est circonscrit à la sphère qu'il remplace. Figure 334.
Il est intéressant de noter qu'un tétraèdre ne peut pas être pavé par des tétraèdres mais peut l'être, avec réserve, par des rhombododécaèdres. La situation est différente pour un cube. Un cube peut être pavé par des cubes. L'espace peut être pavé par des cubes et le cube est le seul solide de Platon ayant cette capacité.
Le pavage du tétraèdre par des rhombododécaèdres doit être compris avec une réserve : l'espace intérieur du tétraèdre est occupé exactement, sans interstices et sans chevauchement, les centres des rhombododécaèdres décrivent exactement les sommets, les arêtes et les faces du tétraèdre. L'assemblage des rhombododécaèdres est limité extérieurement par des faces planes, mais le nombre de celles-ci dépasse 4, alors qu'un tétraèdre est limité par 4 faces planes.
Une semblable réserve n'existe pas dans le cas du pavage d'un cube par des cubes. L'assemblage des cubes donne un cube exactement avec ses 6 faces.
Pour ce qui est du pavage de l'espace par le rhombododécaèdre, il peut être étendu indéfiniment en tous sens.
Si on établit un paralèle avec le pavage bidimensionnel, on note que le triangle régulier peut paver exactement un triangle régulier ou un hexagone régulier et qu'un carré peut paver exactement un carré. Nous n'aborderons pas le pavage par le pentagone.
Autres figures 3D.
Une pyramide de base carrée de 120 boules remplaçant les 120 cubes de la figure 304 serait en équilibre instable, mais 4 pyramides de base carrée de 30 boules sont stables. Les partenaires
des 30 tétrades peuvent y être placés en symétrie quaternaire par rapport à l'axe de l'installation. Le plan de chaque strate est celui de la figure 278, les quadrants étant isolés. Figure 335.
En déplaçant les strates vers l'extérieur selon les diagonales, on obtient une structure en forme d'étoile à 4 branches, qui n'est pas stable d'elle-même et requiert un support. Figure 336.
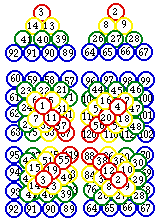
Fig. 335. Quatre pyramides de bases carrées. Les strates par quadrants. Plan et vue de côté. Valeurs de Z.
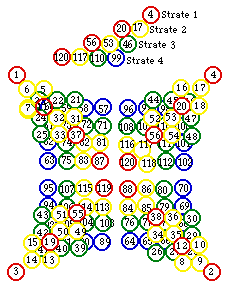
Fig. 336. Structure en étoile à 4 branches. Plan, coupe dans une branche. Valeurs de Z.
Tétraèdres non massifs.
Quatre tétrades de boules s'assemblent en un tronc de tétraèdre. Elles peuvent aussi s'assembler en un tétraèdre, l'une d'elles étant portée par les trois autres et en laissant vide l'espace d'une tétrade : le tétraèdre est non massif. Le tétraèdre a 4 boules d'arête.
Quatre fois 4 tétrades peuvent s'assembler en un tétraèdre non msssif. laissant vide l'espace de 14 tétrades. Le tétraèdre a 8 boules d'arête. D'autres assemblages non massifs sont encore possibles.
On obtient des tétraèdres massifs, ne contenant aucun espace pour y loger des tétrades supplémentaires, avec 1, 5, 14 ou 30 tétrades.
Applications à la classification des éléments. Conclusion.
Ce qui précède devrait suffir à démontrer que tableaux, nombres et géométrie, tels que présentés dans le système du québécium, sont intimement associés à l'organisation de la matière et aux forces électromagnétiques à l'intérieur de l'atome et permettent de comprendre un peu mieux cette organisation et ces forces.
QbSyst2e.24.html
Système du Québécium
Suivant QbSyst2e.25.html
Précédents QbSyst2e.23quater.html QbSyst2e.23bis.html
![]()